摘要:[选做题]在A.B.C.D四小题中只能选做两题.每小题10分.共计20分.请在答题卡指定区域内作答.解答时应写出文字说明.证明过程或演算步骤. A.选修4 - 1:几何证明选讲 如图.在四边形ABCD中.△ABC≌△BAD. 求证:AB∥CD. [解析] 本小题主要考查四边形.全等三角形的有关知识.考查推理论证能力.满分10分. 证明:由△ABC≌△BAD得∠ACB=∠BDA.故A.B.C.D四点共圆.从而∠CBA=∠CDB.再由△ABC≌△BAD得∠CAB=∠DBA.因此∠DBA=∠CDB.所以AB∥CD. B. 选修4 - 2:矩阵与变换 求矩阵的逆矩阵. [解析] 本小题主要考查逆矩阵的求法.考查运算求解能力.满分10分. 解:设矩阵A的逆矩阵为则 即故 解得:. 从而A的逆矩阵为. C. 选修4 - 4:坐标系与参数方程 已知曲线C的参数方程为(为参数.). 求曲线C的普通方程. [解析] 本小题主要考查参数方程和普通方程的基本知识.考查转化问题的能力.满分10分. 解:因为所以 故曲线C的普通方程为:. D. 选修4 - 5:不等式选讲 设≥>0,求证:≥. [解析] 本小题主要考查比较法证明不等式的常见方法.考查代数式的变形能力.满分10分. 证明: 因为≥>0,所以≥0.>0.从而≥0. 即≥. [必做题]第22题.第23题.每题10分.共计20分.请在答题卡指定区域内作答.解答时应写出文字说明.证明过程或演算步骤.
网址:http://m.1010jiajiao.com/timu_id_4003106[举报]
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.A选修4-1:几何证明选讲
如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.
求证:∠ACB=
| 1 |
| 3 |
B选修4-2:矩阵与变换
已知矩阵A=
|
| β |
|
| a |
| a |
| β |
C选修4-3:坐标系与参数方程
已知椭圆C的极坐标方程为ρ2=
| a |
| 3cos2θ+4sin2θ |
D选修4-4:不等式选讲
已知函数f(x)=(x-a)2+(x-b)2+(x-c)2+
| (a+b+c)2 |
| 3 |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,求线段AE的长.
B.(选修4-2:矩阵与变换)
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
|
|
C.(选修4-4:坐标系与参数方程)
以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,建立极坐标系(两种坐标系中取相同的单位长度),已知点A的直角坐标为(-2,6),点B的极坐标为(4,
| π |
| 2 |
| π |
| 4 |
D.(选修4-5:不等式选讲)
设a,b,c,d都是正数,且x=
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵
|
C.(选修4-4:坐标系与参数方程)
已知曲线C1:
|
| π |
| 4 |
| 2 |
(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<
| c |
| 4 |
| c |
| 6 |
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
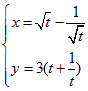 (
(