摘要：9．已知 证:由题设:
网址：http://m.1010jiajiao.com/timu_id_4001373[举报]
已知一几何体的直观图和三视图如下图示：
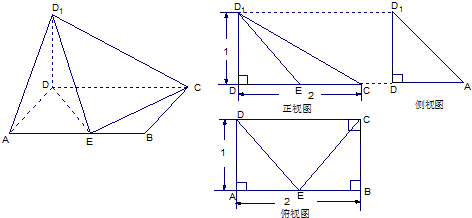
假设点E是AB上的动点，试根据以上图形提供的信息解决以下问题．
（1）三棱锥C-DED1的体积是否与点E的位置有关？说明理由；
（2）当异面直线AD1与EC所成角为60°时，请确定动点E的位置；
（3）在（2）的条件下，求证平面DED1⊥平面D1EC． 查看习题详情和答案>>
假设点E是AB上的动点，试根据以上图形提供的信息解决以下问题．
（1）三棱锥C-DED1的体积是否与点E的位置有关？说明理由；
（2）当异面直线AD1与EC所成角为60°时，请确定动点E的位置；
（3）在（2）的条件下，求证平面DED1⊥平面D1EC． 查看习题详情和答案>>
已知曲线C1：y=
+e（e为自然对数的底数），曲线C2：y=2elnx和直线l：y=2x．
（1）求证：直线l与曲线C1，C2都相切，且切于同一点；
（2）设直线x=t（t＞0）与曲线C1，C2及直线l分别相交于M，N，P，记f（t）=|PM|-|NP|，求f（t）在[e-3，e3]上的最大值；
（3）设直线x=em（m=0，1，2，3┅┅）与曲线C1和C2的交点分别为Am和Bm，问是否存在正整数n，使得A0B0=AnBn？若存在，求出n；若不存在，请说明理由． （本小题参考数据e≈2.7）． 查看习题详情和答案>>
| x2 | e |
（1）求证：直线l与曲线C1，C2都相切，且切于同一点；
（2）设直线x=t（t＞0）与曲线C1，C2及直线l分别相交于M，N，P，记f（t）=|PM|-|NP|，求f（t）在[e-3，e3]上的最大值；
（3）设直线x=em（m=0，1，2，3┅┅）与曲线C1和C2的交点分别为Am和Bm，问是否存在正整数n，使得A0B0=AnBn？若存在，求出n；若不存在，请说明理由． （本小题参考数据e≈2.7）． 查看习题详情和答案>>
“已知：△ABC中，AB=AC，求证：∠B＜90°”．下面写出了用反证法证明这个命题过程中的四个推理步骤：
（1）所以∠A+∠B+∠C＞180°，这与三角形内角和定理相矛盾，；
（2）所以∠B＜90°；
（3）假设∠B≥90°；
（4）那么，由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°
这四个步骤正确的顺序应是（ ）
（1）所以∠A+∠B+∠C＞180°，这与三角形内角和定理相矛盾，；
（2）所以∠B＜90°；
（3）假设∠B≥90°；
（4）那么，由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°
这四个步骤正确的顺序应是（ ）
查看习题详情和答案>>
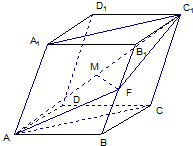已知四棱柱ABCD-A1B1C1D1中的底面是菱形，且∠DAB=∠A1AB=∠A1AD=60°，AD=1，AA1=a，F为棱BB的中点，M为线段AC的中点．设
为数列
的前
项和，
，
.
中，
，求证：
中，
，求证：
，可利用
、