摘要:求曲线在时的导数.
网址:http://m.1010jiajiao.com/timu_id_4000065[举报]
求曲线y=x2+1在点P(1,2)处的切线的斜率k.
探究:用导数的方法求P点的切线的斜率:在P点附近作另一个点Q,先表示出割线PQ的斜率,让后将Q点无限接近于P点,即当Δx趋向于0时,割线PQ的斜率为过P点的切线的斜率.
已知函数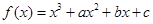 ,曲线
,曲线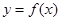 在点
在点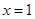 处的切线为
处的切线为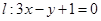 ,若
,若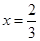 时,
时,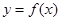 有极值.
有极值.
(1)求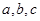 的值;
的值;
(2)求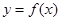 在
在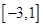 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根据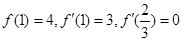 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.
(2)在(1)的基础上,利用导数列表求极值,最值即可.
查看习题详情和答案>>
已知函数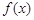 的导函数是
的导函数是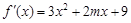 ,
,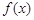 在
在 处取得极值,且
处取得极值,且 .
.
(Ⅰ)求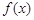 的极大值和极小值;
的极大值和极小值;
(Ⅱ)记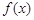 在闭区间
在闭区间 上的最大值为
上的最大值为 ,若对任意的
,若对任意的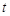
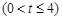 总有
总有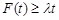 成立,求
成立,求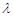 的取值范围;
的取值范围;
(Ⅲ)设 是曲线
是曲线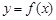 上的任意一点.当
上的任意一点.当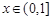 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断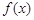 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
查看习题详情和答案>>
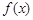 的导函数是
的导函数是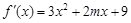 ,
,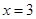 处取得极值,且
处取得极值,且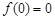 .
.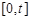 上的最大值为
上的最大值为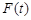 ,若对任意的
,若对任意的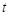
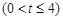 总有
总有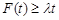 成立,求
成立,求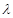 的取值范围;
的取值范围;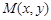 是曲线
是曲线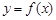 上的任意一点.当
上的任意一点.当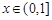 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断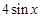 的大小关系,并说明理由.
的大小关系,并说明理由.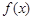 的导函数是
的导函数是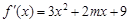 ,
,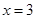 处取得极值,且
处取得极值,且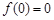 ,
,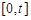 上的最大值为
上的最大值为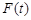 ,若对任意的
,若对任意的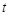
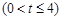 总有
总有 成立,求
成立,求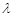 的取值范围;
的取值范围;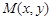 是曲线
是曲线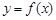 上的任意一点.当
上的任意一点.当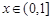 时,求直线OM斜率的最
时,求直线OM斜率的最 的大小关系,并说明理由.
的大小关系,并说明理由.