摘要: 设.b是满足的实数.其中. ⑴求证:, ⑵求证:. 解:(1)由只能 (2)由 由于a.b为正数. . 即 [探索题]已知.求证: (1) 中至少有一个不小于. (2) 若时. ,求证:|p|≤1. [分析]由于题(1)的结论是:三个函数值中“至少有一个不小于 .情况较复杂.会出现多个异向不等式组成的不等式组.一一证明十分繁冗.而结论的反面构成三个同向不等式.结构简单.故采用反证法为宜. 证明假设都小于.则 . 而 .相互矛盾 ∴中至少有一个不小于. (2)由已知得. ∴∴
网址:http://m.1010jiajiao.com/timu_id_3999992[举报]
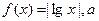 、b是满足
、b是满足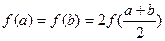 的实数,其中
的实数,其中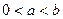 .
.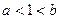 ;(2)求证:
;(2)求证: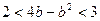 .
.