摘要:研究实例 (1)探讨函数.当无限趋近于2时的变化趋势. 当从左侧趋近于2时.记为:. 1.1 1.3 1.5 1.7 1.9 1.99 1.999 1.9999 2 y=x2 1.21 1.69 2.25 2.89 3.61 3.9601 3.996 3.9996 4 当从右侧趋近于2时, 记为:. 2.9 2.7 2.5 2.3 2.1 2.01 2.001 2.0001 2 y=x2 8.41. 7.29 6.25 5.25 4.41 4.04 4.004 4.0004 4 发现,,因此有. (2)我们再继续看,当无限趋近于1()时的变化趋势: ,当从左侧趋近于1时.即时.. 当从右侧趋近于1时, 即时.. 即. (3)分段函数当x→0的变化趋势. ①x从0的左边无限趋近于0.则的值无限趋近于-1.即 ②x从0的右边无限趋近于0.则的值无限趋近于1. 即 可以看出.并且都不等于.象这种情况.就称当时.的极限不存在.
网址:http://m.1010jiajiao.com/timu_id_3996828[举报]
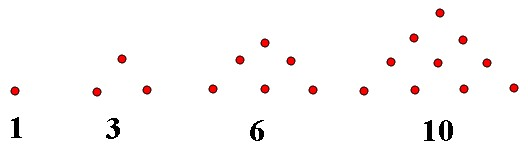
人们通过研究发现1,3,6,10,…这些数能表示三角形,所以将其称为三角形数,类似地,1,4,9,16…这样的数称为正方形数,下列数中既是三角形数又是正方形数的是( )
| A、289 | B、1024 | C、1225 | D、1378 |
已知函数f(x)=
.请完成以下任务:
(Ⅰ)探究a=1时,函数f(x)在区间[0,+∞)上的最大值.为此,我们列表如下
请观察表中y值随x值变化的特点,解答以下两个问题.
(1)写出函数f(x),在[0,+∞)上的单调区间;指出在各个区间上的单调性,并对其中一个区间的单调性用定义加以证明.
(2)请回答:当x取何值时f(x)取得最大值,f(x)的最大值是多少?
(Ⅱ)按以下两个步骤研究a=1时,函数f(x)=
,(x∈R)的值域.
(1)判断函数f(x)的奇偶性;
(2)结合已知和以上研究,画出函数f(x)的大致图象,指出函数的值域.
(Ⅲ)己知a=-1,f(x)的定义域为(-1,1),解不等式f(4-3x)+f(x-
)>0.
查看习题详情和答案>>
| 4x |
| x2+a |
(Ⅰ)探究a=1时,函数f(x)在区间[0,+∞)上的最大值.为此,我们列表如下
| x | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
(1)写出函数f(x),在[0,+∞)上的单调区间;指出在各个区间上的单调性,并对其中一个区间的单调性用定义加以证明.
(2)请回答:当x取何值时f(x)取得最大值,f(x)的最大值是多少?
(Ⅱ)按以下两个步骤研究a=1时,函数f(x)=
| 4x |
| x2+a |
(1)判断函数f(x)的奇偶性;
(2)结合已知和以上研究,画出函数f(x)的大致图象,指出函数的值域.
(Ⅲ)己知a=-1,f(x)的定义域为(-1,1),解不等式f(4-3x)+f(x-
| 3 |
| 2 |
(2012•普陀区一模)设点F是抛物L:y2=2px(p>0)的焦点,P1,P2,…,Pn是抛物线L上的n个不同的点n(n≥3,n∈N*).
(1)当p=2时,试写出抛物线L上三点P1、P2、P3的坐标,时期满足|
|+|
|+|
|=6;
(2)当n≥3时,若
+
+…+
=
,求证:|
|+|
|+…+|
|=np;
(3)当n>3时,某同学对(2)的逆命题,即:“若|
|+|
|+…+|
|=np,则
+
+…+
=
”开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
1.试构造一个说明该命题确实是假命题的反例;
2.对任意给定的大于3的正整数n,试构造该假命题反例的一般形式,并说明你的理由:
3.如果补充一个条件后能使该命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由.
查看习题详情和答案>>
(1)当p=2时,试写出抛物线L上三点P1、P2、P3的坐标,时期满足|
| FP1 |
| FP2 |
| FP3 |
(2)当n≥3时,若
| FP1 |
| FP2 |
| FPn |
| 0 |
| FP1 |
| FP2 |
| FPn |
(3)当n>3时,某同学对(2)的逆命题,即:“若|
| FP1 |
| FP2 |
| FPN |
| FP1 |
| FP2 |
| FPN |
| 0 |
请你就此从以下三个研究方向中任选一个开展研究:
1.试构造一个说明该命题确实是假命题的反例;
2.对任意给定的大于3的正整数n,试构造该假命题反例的一般形式,并说明你的理由:
3.如果补充一个条件后能使该命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由.
已知函数 .请完成以下任务:
.请完成以下任务:
(Ⅰ)探究a=1时,函数f(x)在区间[0,+∞)上的最大值.为此,我们列表如下
请观察表中y值随x值变化的特点,解答以下两个问题.
(1)写出函数f(x),在[0,+∞)上的单调区间;指出在各个区间上的单调性,并对其中一个区间的单调性用定义加以证明.
(2)请回答:当x取何值时f(x)取得最大值,f(x)的最大值是多少?
(Ⅱ)按以下两个步骤研究a=1时,函数 的值域.
的值域.
(1)判断函数f(x)的奇偶性;
(2)结合已知和以上研究,画出函数f(x)的大致图象,指出函数的值域.
(Ⅲ)己知a=-1,f(x)的定义域为(-1,1),解不等式 .
.
查看习题详情和答案>>
 .请完成以下任务:
.请完成以下任务:(Ⅰ)探究a=1时,函数f(x)在区间[0,+∞)上的最大值.为此,我们列表如下
| x | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … | |
| y | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
(1)写出函数f(x),在[0,+∞)上的单调区间;指出在各个区间上的单调性,并对其中一个区间的单调性用定义加以证明.
(2)请回答:当x取何值时f(x)取得最大值,f(x)的最大值是多少?
(Ⅱ)按以下两个步骤研究a=1时,函数
 的值域.
的值域.(1)判断函数f(x)的奇偶性;
(2)结合已知和以上研究,画出函数f(x)的大致图象,指出函数的值域.
(Ⅲ)己知a=-1,f(x)的定义域为(-1,1),解不等式
 .
.查看习题详情和答案>>