题目内容
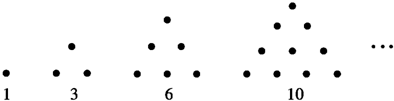
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数．他们研究过1，3，6，10，…，可以用如图的三角形点阵表示，那么第10个点阵表示的数是 ．
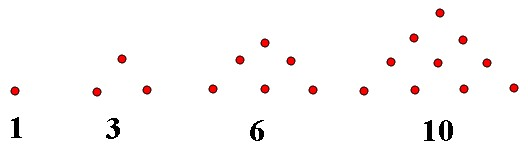
分析：设此数列1，3，6，10，…的通项公式为an，可得a2-a1=3-1=2，a3-a2=6-3=3，a4-a3=10-6=4，…，利用等差数列的通项公式可得an+1-an=2+（n-1）=n+1，再利用“累加求和”即可得出．
解答：解：设此数列1，3，6，10，…的通项公式为an，
则a2-a1=3-1=2，a3-a2=6-3=3，a4-a3=10-6=4，…．
∴数列{an+1-an}是等差数列，首项为2，公差为1．
∴an+1-an=2+（n-1）=n+1，
∴an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=n+（n-1）+…+1
=
．
∴a10=
=55．
故答案为：55．
则a2-a1=3-1=2，a3-a2=6-3=3，a4-a3=10-6=4，…．
∴数列{an+1-an}是等差数列，首项为2，公差为1．
∴an+1-an=2+（n-1）=n+1，
∴an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=n+（n-1）+…+1
=
| n(n+1) |
| 2 |
∴a10=
| 10×11 |
| 2 |
故答案为：55．
点评：本题考查了等差数列的通项公式和“累加求和”等基础知识与基本技能方法，属于基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
