摘要：(一)曲线的切线及切线的斜率 如图3.1-2,当沿着曲线趋近于点时,割线的变化趋势是什么? 我们发现,当点沿着曲线无限接近点即时,割线趋近于确定的位置,这个确定位置的直线称为曲线在点处的切线. 问题: (1)割线的斜率与切线的斜率有什么关系? (2)切线的斜率为多少? 容易知道,割线的斜率是,当点沿着曲线无限接近点时,无限趋近于切线的斜率,即 说明: (1)设切线的倾斜角为, 那么当时,割线的斜率,称为曲线在点处的切线的斜率. 这个概念: ①提供了求曲线上某点切线的斜率的一种方法; ②切线斜率的本质-函数在处的导数. (2)曲线在某点处的切线: 1)与该点的位置有关; 2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线; 3)曲线切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多.
网址：http://m.1010jiajiao.com/timu_id_3995268[举报]
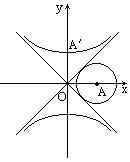
如图，已知双曲线S的两条渐近线过坐标原点且与以点A（
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与A关于直线y=x对称，设直线l过点A，且斜率为k.
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与A关于直线y=x对称，设直线l过点A，且斜率为k. 
（1）求双曲线S的方程；
（2）当k=1时，在双曲线S的上支上求点B，使其与直线l的距离为
；
（3）当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为
，求斜率k的值及相应的点B的坐标.
查看习题详情和答案>>
| |||||||||||||||
，0)为圆心、1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
已知双曲线S的两条渐近线过坐标原点，且与以点A(
，0)为圆心，1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
(1)求双曲线S的方程；
(2)当k＝1时，在双曲线S的上支上求点B，使其与直线l的距离为
；
(3)当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为
，求斜率k的值及相应的点B的坐标．如图．
查看习题详情和答案>>
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
；
，求斜率k的值及相应的点B的坐标，如图.
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
；
，求斜率k的值及相应的点B的坐标，如图.