题目内容
| |||||||||||||||
，0)为圆心、1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
答案：
解析：
解析：
(1) |
解析：由已知可得双曲线的两条渐近线方程为y＝±x， 双曲线S的方程为 |
(2) |
设B(x， 解得x＝ |
(3) |
当0≤k＜1时，双曲线S的上支在直线l的上方，所以点B在直线l的上方．设直线 设 由l上的点A到 因为直线 由方程组 消去y，得(k2－1)x2＋2mkx＋m2－2＝0， 因为k2≠1，所以 △＝4m2k2－4(k2－1)(m2－2) ＝4( ＝8k(3k－2 令△＝0，由0≤k＜1，解得k＝0，k＝ 当k＝0时，m＝ 此时点B的坐标为(0， 当k＝ |
(0，
)．
－
＝1．
)是双曲线S上到直线l：y＝x－
＝
与直线l：y＝k(x－
＝
－k)．
－2＋2k2)
．
时，m＝
，解得x＝2
．此时点B的坐标为(2
练习册系列答案
相关题目
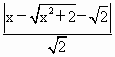双曲线方程为
程序框图，如图所示，已知曲线E的方程为ax2+by2=ab（a，b∈R），若该程序输出的结果为s，则下列命题正确的是
、
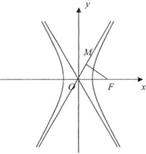
在x轴上，点P在双曲线的左支上，点M在右准线上，且满足
，
．
)，
、
是双曲线虚轴的上、下端点，点A、B是双曲线上不同的两点，且
，
，求直线AB的方程．
=1.