摘要:2.熟练掌握正弦函数.余弦函数.正切函数.余切函数的性质.并能用它研究复合函数的性质,熟练掌握正弦函数.余弦函数.正切函数.余切函数图象的形状.特点.并会用五点画出函数的图象,理解图象平移变换.伸缩变换的意义.并会用这两种变换研究函数图象的变化.
网址:http://m.1010jiajiao.com/timu_id_3994133[举报]
给出下列命题:①若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列;②已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值为2,θ的值为
;③正弦函数在第一象限为单调递增函数;④函数y=2sin(2x-
)的图象的一个对称点是(
,0);其中正确命题的序号是 .(把你认为正确命题的序号都填上)
查看习题详情和答案>>
| π |
| 2 |
| π |
| 6 |
| π |
| 12 |
给出下列五个结论:
①函数y=2sin(2x-
)有一条对称轴是x=
;
②函数y=tanx的图象关于点(
,0)对称;
③正弦函数在第一象限为增函数;
④要得到y=3sin(2x+
)的图象,只需将y=3sin2x的图象左移
个单位;
⑤若sin(2x1-
)=sin(2x2-
),则x1-x2=kπ,其中k∈Z;
其中正确的有
查看习题详情和答案>>
①函数y=2sin(2x-
| π |
| 3 |
| 5π |
| 12 |
②函数y=tanx的图象关于点(
| π |
| 2 |
③正弦函数在第一象限为增函数;
④要得到y=3sin(2x+
| π |
| 4 |
| π |
| 4 |
⑤若sin(2x1-
| π |
| 4 |
| π |
| 4 |
其中正确的有
①②
①②
.(填写正确结论前面的序号)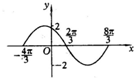 如图,正弦函数图象的相应的解析式为
如图,正弦函数图象的相应的解析式为