题目内容
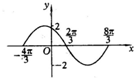 如图,正弦函数图象的相应的解析式为
如图,正弦函数图象的相应的解析式为y=2sin(
+
)
| x |
| 2 |
| 2π |
| 3 |
y=2sin(
+
)
.| x |
| 2 |
| 2π |
| 3 |
分析:设函数的解析式为:y=Asin(ωx+φ),由图象可得:A=2,T=4π,再利用周期公式求出ω的值,即可得到y=2sin(
x+φ),根据题中条件得到函数的图象过点(
,-2),将其代入函数解析式进而求出φ的值得到答案.
| 1 |
| 2 |
| 5π |
| 3 |
解答:解:设函数的解析式为:y=Asin(ωx+φ),
由图象可得:A=2,T=
-(-
)=4π,
∴ω=
=
,
∴函数的解析式为:y=2sin(
x+φ).
因为函数的图象过点(
,0),(
,0),
所以函数的图象过点(
,-2),
所以把点(
,-2)代入函数解析式可得:
×
+φ=2kπ+
,
解得:φ=2kπ+
,
所以取φ=
,
所以所求函数的解析式为y=2sin(
x+
).
故答案为:y=2sin(
x+
).
由图象可得:A=2,T=
| 8π |
| 3 |
| 4π |
| 3 |
∴ω=
| 2π |
| T |
| 1 |
| 2 |
∴函数的解析式为:y=2sin(
| 1 |
| 2 |
因为函数的图象过点(
| 2π |
| 3 |
| 8π |
| 3 |
所以函数的图象过点(
| 5π |
| 3 |
所以把点(
| 5π |
| 3 |
| 1 |
| 2 |
| 5π |
| 3 |
| 3π |
| 2 |
解得:φ=2kπ+
| 2π |
| 3 |
所以取φ=
| 2π |
| 3 |
所以所求函数的解析式为y=2sin(
| 1 |
| 2 |
| 2π |
| 3 |
故答案为:y=2sin(
| 1 |
| 2 |
| 2π |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象确定其解析式,解决此类问题的关键是熟练掌握三角函数周期性,对称性,最值等问题的正确理解,而此类问题的难点是φ的确定,利用的方法是将函数的最值点代入,一般不将函数的平衡点代入因为此时会出现两个答案,必须再结合题中条件去掉一个,因此利用的方法是代入最值点或者是利用等效点的方法也可以.

练习册系列答案
相关题目
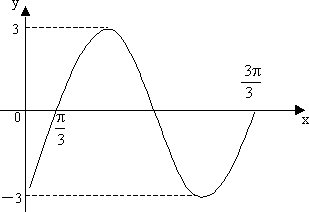


 如图,正弦函数图象的相应的解析式为________.
如图,正弦函数图象的相应的解析式为________.