摘要： 如图11.在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起.A为公共顶点.∠BAC=∠AGF=90°.它们的斜边长为2.若∆ABC固定不动.∆AFG绕点A旋转.AF.AG与边BC的交点分别为D.E(点D不与点B重合,点E不与点C重合),设BE=m.CD=n. (1)请在图中找出两对相似而不全等的三角形.并选取其中一对进行证明. (2)求m与n的函数关系式.直接写出自变量n的取值范围. (3)以∆ABC的斜边BC所在的直线为x轴.BC边上的高所在的直线为y轴.建立平面直角坐标系.在边BC上找一点D.使BD=CE.求出D点的坐标.并通过计算验证BD+CE=DE. 中的等量关系BD+CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由. 六.
网址：http://m.1010jiajiao.com/timu_id_3990492[举报]
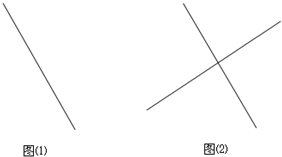
24、在同一平面内有n条直线，任何两条不平行，任何三条不共点．当n=1时，如图（1），一条直线将一个平面分成两个部分；当n=2时，如图（2），两条直线将一个平面分成四个部分；则：当n=3时，三条直线将一个平面分成
查看习题详情和答案>>
7
部分；当n=4时，四条直线将一个平面分成11
部分；若n条直线将一个平面分成an个部分，n+1条直线将一个平面分成an+1个部分．试探索an、an+1、n之间的关系．
为减少交通事故的发生，我市在很多危险路段设置了电子监控仪．如图，在坡脚为30°的公路BC上方的A处，有一电子监控仪，一辆轿车行驶到C处，在同一平面内，由A处测得C处的轿车的俯角为15°，AB垂直于水平面且AB=10m，轿车由C行驶到B处用了1s，如果该路段限速，车速不允许超过40km/h（约11.1m/s），请你求出该轿车的速度，并判断是否超速行驶．（结果精确到0.1m/s，参考数据：| 2 |
| 3 |
为减少交通事故的发生，我市在很多危险路段设置了电子监控仪．如图，在坡脚为30°的公路BC上方的A处，有一电子监控仪，一辆轿车行驶到C处，在同一平面内，由A处测得C处的轿车的俯角为15°，AB垂直于水平面且AB=10m，轿车由C行驶到B处用了1s，如果该路段限速，车速不允许超过40km/h（约11.1m/s），请你求出该轿车的速度，并判断是否超速行驶．（结果精确到0.1m/s，参考数据：
≈1.41，
≈1.73）
查看习题详情和答案>>
≈1.41，≈1.73）
查看习题详情和答案>>
为减少交通事故的发生，我市在很多危险路段设置了电子监控仪．如图，在坡脚为30°的公路BC上方的A处，有一电子监控仪，一辆轿车行驶到C处，在同一平面内，由A处测得C处的轿车的俯角为15°，AB垂直于水平面且AB=10m，轿车由C行驶到B处用了1s，如果该路段限速，车速不允许超过40km/h（约11.1m/s），请你求出该轿车的速度，并判断是否超速行驶．（结果精确到0.1m/s，参考数据：
≈1.41，
≈1.73）