摘要：10．平面内.在中..在上的射影为.则.拓展到空间.在三棱锥中.面在内的射影为.正确的结论是 A． B． C． D．
网址：http://m.1010jiajiao.com/timu_id_3989539[举报]
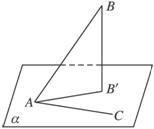
在平面几何里有射影定理：设△ABC的两边AB⊥AC，D是A点在BC上的射影，则AB2＝BD·BC．拓展到空间，在四面体A－BCD中，DA⊥面ABC，点O是A在面BCD内的射影，且O在面BCD内，类比平面三角形射影定理，△ABC，△BOC，△BDC三者面积之间关系为________．
如图，在四棱锥P-ABCD中，顶点P在底面ABCD内的射影恰好落在AB的中点O上，又∠BAD=90°，BC∥AD，且BC：AB：AD=1：2：2．（1）求证：PD⊥AC；
（2）若PO=BC，求直线PD与AB所成的角；
（3）若平面APB与平面PCD所成的角为60°，求
| PO | BC |
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点．（1）求证：EF⊥CD；
（2）求DB与平面DEF所成角的正弦值；
（3）在平面PAD内是否存在一点G，使G在平面PCB上的射影为△PCB的外心，若存在，试确定点G的位置；若不存在，说明理由．
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点．