摘要: 导数与函数的单调性的关系 ㈠与为增函数的关系. 能推出为增函数.但反之不一定.如函数在上单调递增.但.∴是为增函数的充分不必要条件. ㈡时.与为增函数的关系. 若将的根作为分界点.因为规定.即抠去了分界点.此时为增函数.就一定有.∴当时.是为增函数的充分必要条件. ㈢与为增函数的关系. 为增函数.一定可以推出.但反之不一定.因为.即为或.当函数在某个区间内恒有.则为常数.函数不具有单调性.∴是为增函数的必要不充分条件. 函数的单调性是函数一条重要性质.也是高中阶段研究的重点.我们一定要把握好以上三个关系.用导数判断好函数的单调性.因此新教材为解决单调区间的端点问题.都一律用开区间作为单调区间.避免讨论以上问题.也简化了问题.但在实际应用中还会遇到端点的讨论问题.要谨慎处理. ㈣单调区间的求解过程 已知 (1)分析 的定义域, (2)求导数 (3)解不等式.解集在定义域内的部分为增区间 (4)解不等式.解集在定义域内的部分为减区间 我们在应用导数判断函数的单调性时一定要搞清以下三个关系.才能准确无误地判断函数的单调性.以下以增函数为例作简单的分析.前提条件都是函数在某个区间内可导. ㈤函数单调区间的合并 函数单调区间的合并主要依据是函数在单调递增.在单调递增.又知函数在处连续.因此在单调递增.同理减区间的合并也是如此.即相邻区间的单调性相同.且在公共点处函数连续.则二区间就可以合并为以个区间.
网址:http://m.1010jiajiao.com/timu_id_3986161[举报]
已知函数f(x)=lnx-ax2+(2-a)x.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a>0,证明:当![]() 时,
时,![]() ;
;
(Ⅲ)若函数y=f(x)的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:导数![]() (x0)<0.
(x0)<0.
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
查看习题详情和答案>>

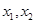 若过两点
若过两点 的直线I与x轴的交点在曲线
的直线I与x轴的交点在曲线 上,求α的值。
上,求α的值。
 ;
; ; (2)求
; (2)求 的最大值与最小值.
的最大值与最小值.