摘要:5.导数的定义 导数定义与求导数的方法是本节的重点.推导导数运算法则与某些导数公式时.都是以此为依据. 对导数的定义.我们应注意以下三点: (1)△x是自变量x在 处的增量. (2)导数定义中还包含了可导或可微的概念.如果△x→0时.有极限.那么函数y=f(x)在点处可导或可微.才能得到f(x)在点处的导数. 在点处可导.那么函数y=f(x)在点处连续.反之不一定成立.例如函数y=|x|在点x=0处连续.但不可导. 由导数定义求导数.是求导数的基本方法.必须严格按以下三个步骤进行: (1)求函数的增量, (2)求平均变化率, (3)取极限.得导数.
网址:http://m.1010jiajiao.com/timu_id_3986159[举报]
已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为f'n(x),且满足:f2(ξ2)=f2(ξ1)+(ξ2-ξ1)f′2[ξ1+
(ξ2-ξ1)](ξ1≠ξ2),λ,ξ1,ξ2为常数.
(Ⅰ)试求λ的值;
(Ⅱ)设函数f2n-1(x)与fn(1-x)的乘积为函数F(x),求F(x)的极大值与极小值;
(Ⅲ)试讨论关于x的方程
=
在区间(0,1)上的实数根的个数.
查看习题详情和答案>>
| 1 |
| λ |
(Ⅰ)试求λ的值;
(Ⅱ)设函数f2n-1(x)与fn(1-x)的乘积为函数F(x),求F(x)的极大值与极小值;
(Ⅲ)试讨论关于x的方程
| f′n(1+x) |
| f′n+1(1+x) |
| λn-1 |
| λn+1-1 |
 ,
, ,其导函数记为
,其导函数记为 ,
, ,求
,求 的极大值与极小值;
的极大值与极小值; 的方程
的方程 在区间
在区间 上的实数根的个数。
上的实数根的个数。 ,
, ,其导函数记为
,其导函数记为 ,且满足:
,且满足: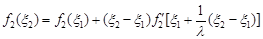
 ,
, 为常数.
为常数. 的值;
的值;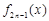 与
与 的乘积为函数
的乘积为函数 ,求
,求 的方程
的方程 在区间
在区间 上的实数根的个数.
上的实数根的个数. ,
,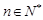 ,其导函数记为
,其导函数记为 ,
, ,求
,求 的极大值与极小值;
的极大值与极小值; 的方程
的方程 在区间
在区间 上的实数根的个数。
上的实数根的个数。 (ξ1≠ξ2),λ,ξ1,ξ2为常数.
(ξ1≠ξ2),λ,ξ1,ξ2为常数. 在区间(0,1)上的实数根的个数.
在区间(0,1)上的实数根的个数.