摘要: 解:画出正常水位时的桥.船的示意图如图1,涨水后桥.船的示意图如图2.以正常水位时河道中央为原点.建立如图2所示的坐标系. 设桥拱圆顶的圆心O1(0.y1).桥拱半径为r.则桥拱圆顶在坐标系中的方程为x2+(y-y1)2=r2. 桥拱最高点B的坐标为(0.9).桥拱与原始水线的交点A的坐标为.圆O1过点A.B.因此 02+(9-y1)2=r2.112+(0-y1)2=r2. 两式相减后得 121+18y1-81=0. y1=-»-2.22, 回代到两个方程之一.即可解出r»11.22. 所以桥拱圆顶的方程是 x2+(y+2.22)2=125.94. 当船行驶在河道的正中央时.船顶最宽处角点C的坐标为(2.y).使船能通过桥洞的最低要求.是点C正好在圆O1上.即22+(y+2.22)2=125.94.解出 y»8.82. 扣除水面上涨的2.70. 点C距水面为8.82-2.70=6.12. ∴船身在水面以上原高6.5.为使船能通过桥洞.应降低船身6.5-6.12=0.38(m)以上
网址:http://m.1010jiajiao.com/timu_id_3983849[举报]
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面为4m,拱圈内水面宽12m,一条船在水面以上部分高2.5m,船顶部宽4m,故通行无阻,近日水位暴涨了1.7m,为此,必须加重船载,降低船身,才能通过桥洞.试问:船身应该降低多少?
查看习题详情和答案>>
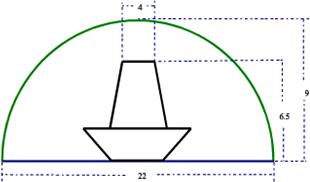 河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:| 9877 |
 已知函数f(x)=x2+|x-a|+1,(x∈R).
已知函数f(x)=x2+|x-a|+1,(x∈R).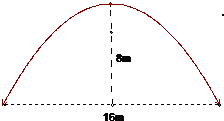 如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.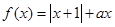 (
(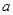 ∈R).
∈R). 的图象;
的图象;