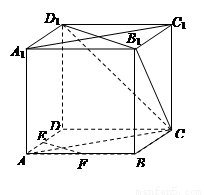
摘要:19. 在长方体中..过..三点的平面截去 长方体的一个角后.得到如图所示的几何体.且这个几何体的体 积为. (I)求棱的长, (Ⅱ)在线段上是否存在点P.使直线与垂直.如果存在.求线段的长.如果不存在.请说明理由, (Ⅲ)求平面与平面所成二面角的余弦值.
网址:http://m.1010jiajiao.com/timu_id_3983324[举报]
(本小题满分12分)如图,在正方体 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)如果 ,一个动点从点
,一个动点从点 出发在正方体的表面上依次经过棱
出发在正方体的表面上依次经过棱 、
、 、
、 、
、 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.

查看习题详情和答案>>
(本小题满分12分)
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1 D1. 过EH的平面与棱BB1,CC1相交,交点分别为F,G。
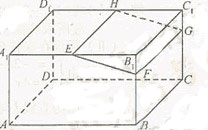
(I) 证明:AD∥平面EFGH;
(II) 设AB=2AA1 ="2" a .在长方体ABCD-A1B1C1D1内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1上运动且满足EF=a时,求p的最小值.
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1 D1. 过EH的平面与棱BB1,CC1相交,交点分别为F,G。

(I) 证明:AD∥平面EFGH;
(II) 设AB=2AA1 ="2" a .在长方体ABCD-A1B1C1D1内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1上运动且满足EF=a时,求p的最小值.
(本小题满分12分)
已知,在水平平面![]() 上有一长方体
上有一长方体![]() 绕
绕![]() 旋转
旋转![]() 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
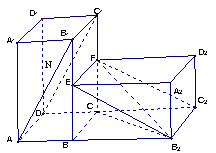 (Ⅱ)当
(Ⅱ)当![]() 时,直线
时,直线![]() 与平面
与平面
![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求
,求![]() 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面
![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,长方体
,长方体![]() 的最
的最
高点离平面![]() 的距离为
的距离为![]() ,请直接写出
,请直接写出![]()
的一个表达式,并注明定义域.
查看习题详情和答案>> ⑴求证:平面
⑴求证:平面 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点.
的中点. ∥平面
∥平面 ;
; ⊥平面
⊥平面 ,一个动点从点
,一个动点从点 、
、 、
、 、
、 、
、 上的点,最终又回到点
上的点,最终又回到点