题目内容
(本小题满分12分)
已知,在水平平面![]() 上有一长方体
上有一长方体![]() 绕
绕![]() 旋转
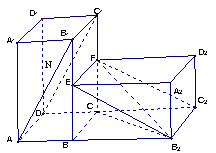
旋转![]() 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
 (Ⅱ)当
(Ⅱ)当![]() 时,直线
时,直线![]() 与平面
与平面
![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求
,求![]() 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面
![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,长方体
,长方体![]() 的最
的最
高点离平面![]() 的距离为
的距离为![]() ,请直接写出
,请直接写出![]()
的一个表达式,并注明定义域.
(12分) 证明:(Ⅰ)延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,

![]() ,
,
![]() ,
,![]()
即 ![]()
又![]()
![]()

![]() ,
,
![]()
![]() 平面
平面![]() 平面
平面![]() ;
;
(Ⅱ)如图,以![]() 所在直线为x轴,
所在直线为x轴,
y轴,z轴,建立空间直角坐标系![]() ,
,
设![]()
![]()
![]()
![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由 ,取
,取![]()
设直线CB1与平面ADC1B1所成的角为θ,
则![]() ,解得
,解得![]()
(Ⅲ)![]()

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目