摘要:(13)抛物线的焦点到准线的距离是 . (14)的展开式的常数项是 . (15)如图.已知正三棱柱的各条棱长都相等.M是侧棱的中点.侧异面直线所成的角的大小是 . (16)设V是已知平面M上所有向量的集合.对于映射记若映射满足:对所有及任意实数都有 称为平面M上的线性变换.现有下列命题: ① 设是平面M上的线性变换. ② 若e是平面M上的单位向量.对是平面M上的线性变换, ③ 对则是平面M上的线性变换, ④ 设是平面M上的线性变换..则对任意实数k均有 其中的真命题是 .
网址:http://m.1010jiajiao.com/timu_id_3982565[举报]
(08年黄冈中学一模理) (本小题满分13分)过抛物线![]() 的焦点F作直线l与抛物线交于A、B.
的焦点F作直线l与抛物线交于A、B.
(1)求证:![]() 不是直角三角形;
不是直角三角形;
(2)当l的斜率为![]() 时,抛物线上是否存在点C,使
时,抛物线上是否存在点C,使![]() 为直角三角形且B为直角(点B位于x轴下方)?若存在,求出所有的点C;若不存在,说明理由.
为直角三角形且B为直角(点B位于x轴下方)?若存在,求出所有的点C;若不存在,说明理由.
 为抛物线
为抛物线 :
: 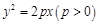 的焦点,
的焦点,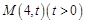 为抛物线
为抛物线 .
.
 的坐标;
的坐标; 的两直线
的两直线 ,
, 与抛物线
与抛物线 ,
,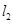 与抛物线
与抛物线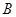 ,记直线
,记直线 的斜率为
的斜率为 .
. ,试求
,试求 为定值.
为定值. ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.