摘要:奇函数:对于函数的定义域内任意一个.都有 (或).则称为奇函数.
网址:http://m.1010jiajiao.com/timu_id_3980737[举报]
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
查看习题详情和答案>>
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
查看习题详情和答案>>
函数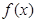 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数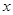 ,在定义域中存在
,在定义域中存在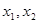 使
使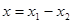 ,
,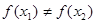 ,且满足以下3个条件。
,且满足以下3个条件。
(1)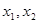 是
是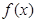 定义域中的数,
定义域中的数,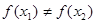 ,则
,则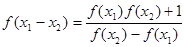
(2)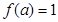 ,(
,(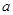 是一个正的常数)
是一个正的常数)
(3)当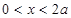 时,
时,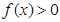 。
。
证明:(1)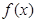 是奇函数;
是奇函数;
(2)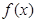 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3)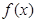 在
在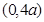 内为减函数。
内为减函数。
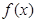 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数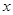 ,在定义域中存在
,在定义域中存在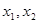 使
使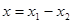 ,
,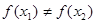 ,且满足以下3个条件。
,且满足以下3个条件。(1)
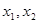 是
是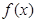 定义域中的数,
定义域中的数,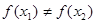 ,则
,则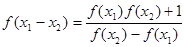
(2)
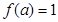 ,(
,(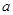 是一个正的常数)
是一个正的常数)(3)当
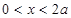 时,
时,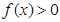 。
。证明:(1)
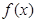 是奇函数;
是奇函数;(2)
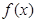 是周期函数,并求出其周期;
是周期函数,并求出其周期;(3)
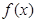 在
在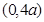 内为减函数。
内为减函数。设函数f(x)的定义域关于原点对称,对定义域内任意的x存在x1和x2,使x=x1-x2,且满足:
(1)f(x1-x2)=
;
(2)当0<x<4时,f(x)>0
请回答下列问题:
(1)判断函数的奇偶性并给出理由;
(2)判断f(x)在(0,4)上的单调性并给出理由.
查看习题详情和答案>>
(1)f(x1-x2)=
| f(x1)-f(x2) | 1+f(x1)•f(x2) |
(2)当0<x<4时,f(x)>0
请回答下列问题:
(1)判断函数的奇偶性并给出理由;
(2)判断f(x)在(0,4)上的单调性并给出理由.
(1)已知函数 的定义域为
的定义域为 ,
, 是奇函数,且当
是奇函数,且当 时,
时, ,若函数
,若函数 的零点恰有两个,则实数
的零点恰有两个,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. 或 或 |
 在其定义域内任意的
在其定义域内任意的 且
且 ,有如下结论:
,有如下结论:①
 ;
;②
 ;
;③
 ;
;④
 .
.上述结论中正确结论的序号是________. 查看习题详情和答案>>