题目内容
函数
的定义域关于原点对称，但不包括数0，对定义域中的任意实数
，在定义域中存在
使
，
，且满足以下3个条件。
（1）是定义域中的数，，则
（2）
，（
是一个正的常数）
（3）当
时，
。
证明：（1）是奇函数；
（2）是周期函数，并求出其周期；
（3）在
内为减函数。
【答案】
证：（1）对定义域中的
，由题设知在定义域中存在
使
，
，
则
∴
为奇函数
（2）因
，∴
，于是
若
，则
若
，则
仍有
。
∴为周期函数，
是它的一个周期。
（3）先证在
内为减函数，事实上，设
，
则
，则
（当
时，
）。
所以
当
时，
，于是
即在
内，也是减函数，从而命题得证。
【解析】略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的定义域关于原点对称，且满足以下三个条件：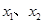
、
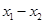是定义域中的数时，有
；
是定义域中的一个数）；
时，
．
与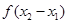
之间的关系，并推断函数
上的单调性，并证明；
时，
的值；②求不等式
的解集． 
的定义域关于原点对称，但不包括数0，对定义域中的任意实数
，在定义域中存在
使
，
，且满足以下3个条件。
，（
是一个正的常数）
时，
。
内为减函数。