摘要：73．设函数. (1)求f(x)的单调区间, (2)若当x∈[-2.2]时.不等式f(x)＞m恒成立.求实数m的取值范围.
网址：http://m.1010jiajiao.com/timu_id_3979175[举报]
设函数f(x)=
x2-lnx （x＞0），其中a为非零常数．
（1）当a=1时，求函数f（x）的单调区间；
（2）若a＞0，过点P(
，0)作函数y=f（x）的导函数y=f′（x）的图象的切线，问这样的切线可作几条？并加以证明．
（3）当x∈[1，2]时，不等式f（x）＞2恒成立，求a的取值范围．
查看习题详情和答案>>
| 1 |
| 2a |
（1）当a=1时，求函数f（x）的单调区间；
（2）若a＞0，过点P(
| a |
（3）当x∈[1，2]时，不等式f（x）＞2恒成立，求a的取值范围．
设函数f(x)=alnx+
，a∈R．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当a＞0时，若对任意x＞0，不等式f（x）≥2a成立，求a的取值范围；
（Ⅲ）当a＜0时，设x1＞0，x2＞0，试比较f（
）与
的大小并说明理由．
查看习题详情和答案>>
| 1 |
| x |
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当a＞0时，若对任意x＞0，不等式f（x）≥2a成立，求a的取值范围；
（Ⅲ）当a＜0时，设x1＞0，x2＞0，试比较f（
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
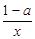－1. 
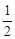时, 求函数f(x)的单调区间；
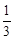时, 设函数g(x)=x2－2bx－
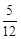, 若对于
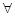x1∈
, 
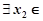[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.（e是自然对数的底, e＜
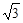+1）.