摘要：判断f(x)=|x|.y=x的单调性并证明.

网址：http://m.1010jiajiao.com/timu_id_3979096[举报]

已知函数f(x)=|

-1|
（1）判断f（x）在[1，+∞）上的单调性，并证明你的结论；
（2）若集合A={y|y=f（x），

≤x≤2}，B=[0，1]，试判断A与B的关系；
（3）若存在实数a、b（a＜b），使得集合{y|y=f（x），a≤x≤b}=[ma，mb]，求非零实数m的取值范围．查看习题详情和答案>>

设函数f（x）的定义域为（0，+∞）且对任意正实数x、y都有f（xy）=f（x）+f（y）恒成立．已知f（2）=1且x＞1时f（x）＞0．
（1）求f（

）的值；
（2）判断f（x）在（0，+∞）上的单调性，并证明；
（3）一个各项均为正数的数列{a_n}满足f（S_n）=f（a_n）+f（a_n+1）-1（n∈N^*），其中S_n是数列{a_n}的前n项和，求{a_n}的通项公式．

查看习题详情和答案>>

函数y=f（x）对于任意正实数x、y，都有f（xy）=f（x）•f（y），当x＞1时，0＜f（x）＜1，且f（2）=

．
（1）求证：f(x)f(

)=1(x＞0)；
（2）判断f（x）在（0，+∞）的单调性；并证明；
（3）若f（m）=3，求正实数m的值．

查看习题详情和答案>>

函数y=f（x）对于任意正实数x、y，都有f（xy）=f（x）•f（y），当x＞1时，0＜f（x）＜1，且f（2）= $数学公式$ ．
（1）求证： $数学公式$ ；
（2）判断f（x）在（0，+∞）的单调性；并证明；
（3）若f（m）=3，求正实数m的值．

查看习题详情和答案>>

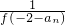设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{a_n}满足f（a_n+1）= $数学公式$ （n∈N^）
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N^，s≠t，使得点（t，a_s）、（s，a_t）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，a _n＞f（0）恒成立？若存在，求出M的最小值，若不存在，请说明理由．

查看习题详情和答案>>