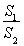摘要：如图所示.抛物线y=4-x2与直线y=3x的两交点为A.B.点P在抛物线上从A向B运动. (1)求使△PAB的面积最大的P点的坐标(a,b); (2)证明由抛物线与线段AB围成的图形.被直线x=a分为面积相等的两部分. (1)解 解方程组.得x1=1,x2=-4. ∴抛物线y=4-x2与直线y=3x的交点为 A. ∴P点的横坐标a∈. 点P(a,b)到直线y=3x的距离为d=, ∵P点在抛物线上.∴b=4-a2. =·(4-3a-a2)′= =0, ∴a=-.即当a=-时.d最大. 这时b=4-=, ∴P点的坐标为(-,)时.△PAB的面积最大. (2)证明 设上述抛物线与直线所围成图形的面积为S, 位于x=-右侧的面积为S1. S=(4-x2-3x)dx=, S1=(4-x2-3x)dx=, ∴S=2S1,即直线x=-平分抛物线与线段AB围成的图形的面积.
网址：http://m.1010jiajiao.com/timu_id_3976830[举报]
如图所示，抛物线y=4-x2与直线y=3x的两交点为A、B，点P在抛物线上从A向B运动.
（1）求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形，被直线x=a分为面积相等的两部分.
查看习题详情和答案>>如图所示，抛物线y=4-x2与直线y=3x的两交点为A、B，点P在抛物线上从A向B运动.
（1）求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形，被直线x=a分为面积相等的两部分.
（1）求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形，被直线x=a分为面积相等的两部分.
如图X15－3所示，已知圆C1：x2＋(y－1)2＝4和抛物线C2：y＝x2－1，过坐标原点O的直线与C2相交于点A，B，定点M的坐标为(0，－1)，直线MA，MB分别与C1相交于点D，E.
(1)求证：MA⊥MB；
(2)记△MAB，△MDE的面积分别为S1，S2，若
＝λ，求λ的取值范围．
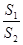＝λ，求λ的取值范围．
