摘要：9．求证:a3+b3+c3≥(a2+b2+c2)(a+b+c)． 证明:∵a2+b2≥2ab.∴(a2+b2)(a+b)≥2ab(a+b). ∴a3+b3+a2b+ab2≥2a2b+2ab2. ∴a3+b3≥a2b+ab2. 同理:b3+c3≥b2c+bc2.a3+c3≥a2c+ac2. 将三式相加得: 2(a3+b3+c3)≥a2b+ab2+b2c+bc2+a2c+ac2. ∴3(a3+b3+c3)≥(a3+a2b+a2c)+(b3+b2a+b2c)+(c3+c2a+c2b)＝(a+b+c)(a2+b2+c2). ∴a3+b3+c3≥(a2+b2+c2)(a+b+c)．
网址：http://m.1010jiajiao.com/timu_id_3971621[举报]
（I）设a＞0，b＞0求证：a3+b3≥a2b+ab2
（II）设a＞0，b＞0，c＞0，且a，b，c不且相等，求证：lg
+lg
+lg
＞lga+lgb+lgc．
查看习题详情和答案>>
（II）设a＞0，b＞0，c＞0，且a，b，c不且相等，求证：lg
| a+b |
| 2 |
| b+c |
| 2 |
| c+a |
| 2 |
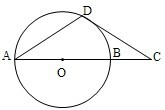本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A：AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC．
B：在平面直角坐标系xOy中，已知点A（0，0），B（-2，0），C（-2，1）．设k为非零实数，矩阵M=
|
|
C：在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切，求实数a的值．
D：设a、b是非负实数，求证：a3+b3≥
| ab |
（2011•南京模拟）A．选修4-1几何证明选讲