摘要:已知=.=. (1)设f(x)= ·.求f(x)的最小正周期和单调递减区间, (2)设有不相等的两个实数x1.x2∈.且f(x1)=f(x2)=1.求x1+x2的值. 解:(1)由f(x)=·得 f(x)=+·2cos =cos2-sin2-2sincos =cosx-sinx =cos(x+). 所以f(x)的最小正周期T=2π. 又由2kπ≤x+≤π+2kπ.k∈Z. 得-+2kπ≤x≤+2kπ.k∈Z. 故f(x)的单调递减区间是[-+2kπ.+2kπ](k∈Z). (2)由f(x)=1得cos(x+)=1.故cos(x+)=. 又x∈.于是有x+∈.得x1=0.x2=-. 所以x1+x2=-.
网址:http://m.1010jiajiao.com/timu_id_3971432[举报]
已知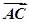 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
),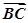 =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)=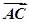 ·
·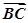 ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈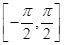 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
查看习题详情和答案>>
已知 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈ ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).(1)设f(x)=
 ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;(2)设有不相等的两个实数x1,x2∈
 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值. 已知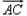 =(cos
=(cos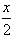 +sin
+sin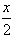 ,-sin
,-sin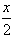 ),
),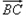 =(cos
=(cos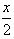 -sin
-sin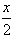 ,2cos
,2cos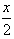 ),
),
(1)设f(x)=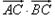 ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈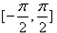 ,且f(x1)=f(x2)=1,求x1+x2的值。
,且f(x1)=f(x2)=1,求x1+x2的值。
查看习题详情和答案>>
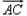 =(cos
=(cos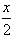 +sin
+sin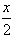 ,-sin
,-sin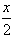 ),
),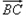 =(cos
=(cos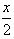 -sin
-sin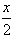 ,2cos
,2cos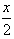 ),
), (1)设f(x)=
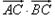 ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;(2)设有不相等的两个实数x1,x2∈
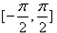 ,且f(x1)=f(x2)=1,求x1+x2的值。
,且f(x1)=f(x2)=1,求x1+x2的值。