题目内容
已知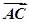 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
),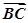 =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)=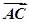 ·
·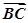 ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈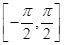 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
【答案】
(1) T=2π
f(x)的单调递减区间是[- +2kπ,
+2kπ,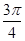 +2kπ](k∈Z)
+2kπ](k∈Z)
(2) x1+x2=-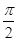
【解析】本试题主要是考查了向量的数量积公式以及三角函数的图像与性质的综合运用。注意解三角方程,要看范围。
解:(1)由f(x)=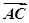 ·
·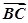 得
得
f(x)=(cos +sin
+sin )·(cos
)·(cos -sin
-sin )+(-sin
)+(-sin )·2cos
)·2cos
=cos2 -sin2
-sin2 -2sin
-2sin cos
cos =cosx-sinx=
=cosx-sinx= cos(x+
cos(x+ ),...........4分
),...........4分
所以f(x)的最小正周期T=2π.............6分
又由2kπ≤x+ ≤π+2kπ,k∈Z,
≤π+2kπ,k∈Z,
得- +2kπ≤x≤
+2kπ≤x≤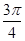 +2kπ,k∈Z.
+2kπ,k∈Z.
故f(x)的单调递减区间是[- +2kπ,
+2kπ,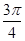 +2kπ](k∈Z) ……..8分
+2kπ](k∈Z) ……..8分
(2)由f(x)=1得 cos(x+
cos(x+ )=1,故cos(x+
)=1,故cos(x+ )=
)=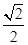 ……10分
……10分
又x∈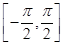 ,于是有x+
,于是有x+ ∈
∈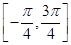 ,得x1=0,x2=-
,得x1=0,x2=-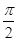 ,
,
所以x1+x2=-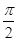

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 =(cos
=(cos +sin
+sin =(cos
=(cos ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.