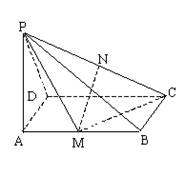
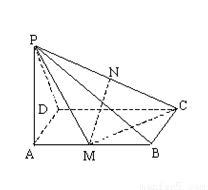
摘要: 如图所示.四棱锥P-ABCD中.AB⊥AD.AD⊥DC.PA⊥底面ABCD.PA=AD=DC=AB=1.M为PC的中点.N点在AB上且AN=NB. (1)证明:MN∥平面PAD, (2)求直线MN与平面PCB所成的角. 解:(1)证明:过M作ME∥CD交PD于E. 连接AE. ∵AN=NB. ∴AN=AB=DC=EM. 又EM∥DC∥AB.∴EMAN. ∴AEMN为平行四边形. ∴MN∥AE.又AE⊂平面PAD.MN⊄平面PAD. ∴MN∥平面PAD. (2)过N点作NQ∥AP交BP于点Q.NF⊥CB交CB于点F. 连接QF.过N点作NH⊥QF交QF于H.连接MH. 易知QN⊥平面ABCD.∴QN⊥BC.而NF⊥BC. ∴BC⊥平面QNF. ∴BC⊥NH.而NH⊥QF.∴NH⊥平面PBC. ∴∠NMH为直线MN与平面PCB所成的角. 通过计算可得MN=AE=.QN=.NF=. ∴NH===. ∴sin∠NMH==.∴∠NMH=60°. ∴直线MN与平面PCB所成的角为60°.
网址:http://m.1010jiajiao.com/timu_id_3971414[举报]
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
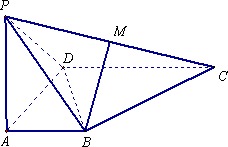
(1)求证:BM∥平面PAD;
(2)求证:面PDC⊥面PAD
(3)在侧面PAD内找一点N,使MN⊥平面PBD.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.

(1)求证:BM∥平面PAD;
(2)求证:面PDC⊥面PAD
(3)在侧面PAD内找一点N,使MN⊥平面PBD.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.