题目内容
如图所示，四棱锥P－ABCD中，AB⊥AD，CD⊥AD，PA⊥底面ABCD，PA＝AD＝CD＝2AB＝2，M为PC的中点．
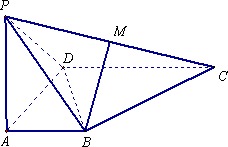
(1)求证：BM∥平面PAD；
(2)求证：面PDC⊥面PAD
(3)在侧面PAD内找一点N，使MN⊥平面PBD．
答案：
解析：
解析：
|
解：(1)
(2)由(1)知 ∵ ∴面PDC⊥面PAD (3)由(2)知 ∵  ， ，
∵ 作 作 |
是
的中点，取PD的中点
，则
，又
四边形
为平行四边形
∥
，
为平行四边形
，又
，同理
，
为矩形
，又
故
交
于
，在矩形
内，
，
，
，
练习册系列答案
阅读快车系列答案
相关题目
如图所示，四棱锥P-ABCD的底面为直角梯形，∠ADC=∠DCB=90°，AD=1，BC=3，PC=CD=2，PC⊥底面ABCD，E为AB的中点．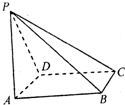
如图所示，四棱锥P-ABCD的底面是一个矩形，AB=3．AD=1．又PA⊥AB，PA=4，
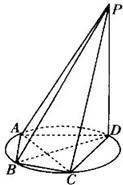如图所示，四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径，∠ABD=60°，∠BDC=45°，△ADP～△BAD．
（2012•烟台一模）如图所示，四棱锥P-ABCD中，ABCD为正方形，PA⊥AD，E，F，G分别是线段PA，PD，CD的中点．
如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E为PC的中点，PA=AD=AB=1．