摘要：已知{an}是一个等差数列.且a2＝1.a5＝-5. (1)求数列{an}的通项an, (2)求{an}前n项和Sn的最大值. 解:(1)设{an}的公差为d. 由已知条件得. 所以an＝a1+(n-1)d＝-2n+5. (2)Sn＝na1+d＝-n2+4n＝4-(n-2)2. 所以n＝2时.Sn取到最大值4.
网址：http://m.1010jiajiao.com/timu_id_3971264[举报]
本小题满分12分）
已知等差数列{an}的首项a1＝1，公差d＞0，且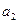
、
、
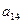分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设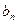
＝
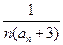（n∈N*），
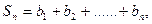求
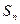
本小题满分12分）
已知等差数列{an}的首项a1＝1，公差d＞0，且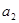
、
、
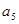分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设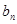
＝
（n∈N*），
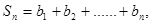求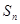
查看习题详情和答案>>
本小题满分12分）
已知等差数列{an}的首项a1＝1，公差d＞0，且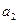
、
、
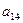分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设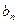
＝
（n∈N*），
求
已知等差数列{an}的首项a1＝1，公差d＞0，且
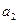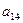、、分别是一个等比数列的第二项、第三项、第四项．（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设
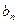＝（n∈N*）， 求（本小题满分12分）
（理）已知Sn是正数数列{an}的前n项和，S12，S22、……、Sn2 ……，是以3为首项，以1为公差的等差数列；数列{bn}为无穷等比数列，其前四项之和为120，第二项与第四项之和为90．
(I)求an、bn；(II)从数列{
}中能否挑出唯一的无穷等比数列，使它的各项和等于
．若能的话，请写出这个数列的第一项和公比?若不能的话，请说明理由．
|
已知{an}是一个公差大于0的等差数列，且满足a3a6＝55, a2+a7＝16.
(Ⅰ)求数列{an}的通项公式：
（Ⅱ）若数列{an}和数列{bn}满足等式：an＝＝
，求数列{bn}的前n项和Sn