摘要:已知椭圆上两点A.B.直线上有两点C.D.且ABCD是正方形.此正方形外接圆为x2+y2-2y-8=0.求椭圆方程和直线的方程.
网址:http://m.1010jiajiao.com/timu_id_3970700[举报]
已知椭圆![]() (a>b>0)的一个焦点与抛物线y2=
(a>b>0)的一个焦点与抛物线y2=![]() 的焦点F重合,且椭圆短轴的两个端点与F构成正三角形.
的焦点F重合,且椭圆短轴的两个端点与F构成正三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点(1,0)的直线l与椭圆交于不同两点P、Q,试问在x轴上是否存在定点E(m,0),使![]() 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且
(a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且![]() 是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为
是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为![]()
(1)求椭圆C的方程;
(2)与两坐标轴都不垂直的直线l:![]() 交椭圆C于E,F两点,且以线段EF为直径的圆恒过坐标原点,当△OEF面积的最大值时,求直线l的方程.
交椭圆C于E,F两点,且以线段EF为直径的圆恒过坐标原点,当△OEF面积的最大值时,求直线l的方程.
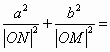 ________.
________.