13．已知的外心为..为的外接圆上且在内部的任意一点.以为直径的圆分别与交于点. 分别与或其延长线交于点.求证三点共线. 证明连.与交于点.由于.因此是等腰三角形.所以,.于是可得.从而有在的中垂——青夏教育精英家教网——

摘要：13．已知的外心为..为的外接圆上且在内部的任意一点.以为直径的圆分别与交于点. 分别与或其延长线交于点.求证三点共线. 证明连.与交于点.由于.因此是等腰三角形.所以,.于是可得.从而有在的中垂线上.由于.在的中垂线上.于是有.即三点共线.

网址：http://m.1010jiajiao.com/timu_id_3963737[举报]

的外接圆上且在

内部的任意一点，以

为直径的圆分别与

或其延长线交于点

三点共线。查看习题详情和答案>>

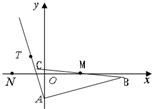已知△ABC的边AB所在直线的方程为x-3y-6=0，M（2，0）满足

，点T（-1，1）在AC所在直线上且

=0．
（1）求△ABC外接圆的方程；
（2）一动圆过点N（-2，0），且与△ABC的外接圆外切，求此动圆圆心的轨迹方程Γ；
（3）过点A斜率为k的直线与曲线Γ交于相异的P，Q两点，满足

＞6，求k的取值范围．查看习题详情和答案>>

已知△ABC的外接圆的圆心为O，半径为1，若

方向上的投影为（　　）

查看习题详情和答案>>

=1（a＞b＞0）的上下焦点分别为F₁，F₁，短轴两个端点为P，P₁，且四边形F₁PF₂P₁是边长为2的正方形．
（1）求椭圆方程；
（2）设△ABC，AC=2

=1（a＞b＞0）在x轴上方的顶点，当AC在直线y=-1上运动时，求△ABC外接圆的圆心Q的轨迹E的方程；
（3）过点F（0，

）作互相垂直的直线l₁l₂，分别交轨迹E于M，N和R，Q．求四边形MRNQ的面积的最小值．

查看习题详情和答案>>

已知椭圆（）的两个焦点分别为，过点的直线与椭圆相交于点A,B两点，且

（Ⅰ求椭圆的离心率

（Ⅱ）直线AB的斜率；

（Ⅲ）设点C与点A关于坐标原点对称，直线上有一点H(m,n)()在的外接圆上，求的值。

查看习题详情和答案>>