题目内容

已知△ABC的外接圆的圆心为O，半径为1，若
AB
+
AC
=2
AO
，且|
OA
|=|
AC
|，则向量
AB
在向量
BC
方向上的投影为（　　）
分析：利用已知可得四边形ABDC是矩形，利用|
OA
|=|
AC
|，可得△OAC是等边三角形．于是向量
AB
在向量
BC
方向上的投影=|
AB
|cos(180°-30°)，得出即可．
解答：解：如图所示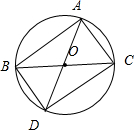，延长AO交⊙O于点D．连接BD、CD．
∵
AB
+
AC
=2
AO
，∴
AB
+
AC
=
AD
，∴四边形ABDC是矩形．
∵|
OA
|=|
AC
|，∴△OAC是等边三角形．
∴∠ACB=60°，又∠BAC=90°．
∴∠ABC=30°．
∵半径为1，即BC=2．∴AB=
3
．
∴向量
AB
在向量
BC
方向上的投影=|
AB
|cos(180°-30°)=
3
×(-
3
2
)=-
3
2
．
故选D．
点评：熟练掌握向量的平行四边形法则、矩形的定义、等边三角形的定义、向量投影的意义等是解题的关键．
练习册系列答案
相关题目
已知△ABC的外接圆的圆心O，BC＞CA＞AB，则
OA
•
OB
，
OA
•
OC
，
OB
•
OC
的大小关系为
 
．
已知△ABC的外接圆的半径为
2
，内角A，B，C的对边分别为a，b，c，又向量
m
=(sinA-sinC，b-a)，
n
=(sinA+sinC，
2
4
sinB)，且
m
⊥
n
，
（I）求角C；
（II）求三角形ABC的面积S的最大值．
已知△ABC的外接圆半径R为6，面积为S，a、b、c分别是角A、B、C的对边设S=a2-(b-c)2，sinB+sinC=
43
．
（I）求sinA的值；
（II）求△ABC面积的最大值．
已知△ABC的外接圆半径为1，角A，B，C的对边分别为a，b，c．向量
m
=(a，4cosB)，
n
=(cosA，b)满足
m
∥
n
．
（1）求sinA+sinB的取值范围；
（2）若A∈(0，
π
3
)，且实数x满足abx=a-b，试确定x的取值范围．
已知△ABC的外接圆圆心为O，BC＞CA＞AB．则（　　）
A、
OA
•
OB
＞
OA
•
OC
＞
OB
•
OC
B、
OA
•
OB
＞
OB
•
OC
＞
OC
•
OA
C、
OC
•
OB
＞
OA
•
OC
＞
OB
•
OA
D、
OA
•
OC
＞
OB
•
OC
＞
OA
•
OB

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网