摘要：9．若是边长为的正三角形的边上的点.与的内切圆半径分别为.若.则满足条件的点有两个.分别设为.则之间的距离为 . 答 . 设.由余弦定理得.一方面..另一方面..解得.同理可得.从而有.当时.有最大值.且最大值为.所以.由于.所以.设两个根分别为.则.
网址：http://m.1010jiajiao.com/timu_id_3963733[举报]
是边长为
的正三角形
的边
上的点，
与
的内切圆半径分别为
，若
，则满足条件的点
，则
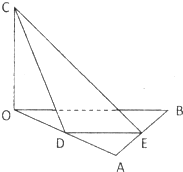△OAB是边长为4的正三角形，CO⊥平面OAB且CO=2，设D、E分别是OA、AB的中点．（1）求证：OB∥平面CDE；
（2）求三棱锥O-CDE的体积；
（3）在CD上是否存在点M，使OM⊥平面CDE，若存在，则求出M点的位置，若不存在，请说明理由．
的值恒为