题目内容
若P是边长为2的正三角形ABC边BC上的动点,则| AP |
| AB |
| AC |
分析:画出图形,作出以向量
为对角线的平行四边形,设出图中的比例关系,表示出向量
,然后计算
•(
+
),注意两个比例系数之和为1,可求得数量积为定值.
| AP |
| AP |
| AP |
| AB |
| AC |
解答: 解:如图P是边长为2的正三角形ABC边BC上的动点,
解:如图P是边长为2的正三角形ABC边BC上的动点,
过P作EP∥AB,交AC于E,FP∥AC交AB于F,
设m=
,n=
,由于ABC是正三角形,
所以 m+n=1.
所以
•(
+
)=(m
+n
)•(
+
)
=m
2+n
2+(m+n)
•
=4m+4n+(m+n)×2×2×
=6(m+n)
=6.
故答案为:6.
 解:如图P是边长为2的正三角形ABC边BC上的动点,
解:如图P是边长为2的正三角形ABC边BC上的动点,过P作EP∥AB,交AC于E,FP∥AC交AB于F,
设m=
| AE |
| AC |
| AF |
| AB |
所以 m+n=1.
所以
| AP |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
=m
| AB |
| AC |
| AB |
| AC |
=4m+4n+(m+n)×2×2×
| 1 |
| 2 |
=6(m+n)
=6.
故答案为:6.
点评:本题考查平面向量数量积的含义与物理意义,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

 ,
是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°?
若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
,
是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°?
若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.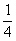 ,则侧棱PA与底面所成角的正切值是
,则侧棱PA与底面所成角的正切值是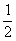 C.
C.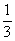 D.
D.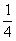 ,则侧棱PA与底面所成角的正切值是
,则侧棱PA与底面所成角的正切值是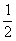 C.
C.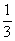 D.
D.