摘要:9.如图.在平面直角坐标系xOy中.以Ox轴为始边作两个锐角α.β.它们的终边分别 与单位圆相交于A.B两点.已知A.B的横坐标分别为.. (1)求tan(α+β)的值, (2)求α+2β的值. 解:(1)由已知条件及三角函数的定义可知.cosα=.cosβ=.因α为锐角.故sinα >0.从而sinα==.同理可得sinβ=.因此tanα=7.tanβ=. 所以tan(α+β)===-3. (2)tan(α+2β)=tan[(α+β)+β]==-1. 又0<α<.0<β<.故0<α+2β<. 从而由tan(α+2β)=-1得α+2β=. 题组四 公式的综合应用
网址:http://m.1010jiajiao.com/timu_id_3959043[举报]
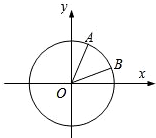 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是
| ||
| 10 |
2
| ||
| 5 |
(1)求tan(α+β)的值;
(2)求α+2β的值. 查看习题详情和答案>>
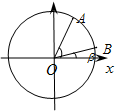 如图,在平面直角坐标系xOy中,以x为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为
如图,在平面直角坐标系xOy中,以x为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为
| ||
| 5 |
7
| ||
| 10 |
(1)求tan(α+β)的值;
(2)求2α+β的值. 查看习题详情和答案>>
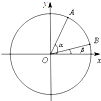 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α、β,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α、β,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为| 1 | ||
|
| 1 | ||
5
|
3
3
. 如图,在平面直角坐标系xOy中,以Ox轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知点A的横坐标为
如图,在平面直角坐标系xOy中,以Ox轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知点A的横坐标为 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为