题目内容
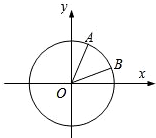 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是
| ||
| 10 |
2
| ||
| 5 |
(1)求tan(α+β)的值;
(2)求α+2β的值.
分析:(1)先由已知条件得cosα=
,cosβ=
;再求sinα、sinβ进而求出tanα、tanβ;
最后利用tan(α+β)=
解之.
(2)利用第一问把tan(α+2β)转化为tan[(α+β)+β]求之,再根据α+2β的范围确定角的值.
| ||
| 10 |
2
| ||
| 5 |
最后利用tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
(2)利用第一问把tan(α+2β)转化为tan[(α+β)+β]求之,再根据α+2β的范围确定角的值.
解答:解:(1)由已知条件即三角函数的定义可知cosα=
,cosβ=
,
因为α为锐角,则sinα>0,从而sinα=
=
同理可得sinβ=
=
,
因此tanα=7,tanβ=
.
所以tan(α+β)=
=
=-3;
(2)tan(α+2β)=tan[(α+β)+β]=
=-1,
又0<α<
,0<β<
,故0<α+2β<
,
所以由tan(α+2β)=-1得α+2β=
.
| ||
| 10 |
2
| ||
| 5 |
因为α为锐角,则sinα>0,从而sinα=
| 1-cos2α |
7
| ||
| 10 |
同理可得sinβ=
| 1-cos2β |
| ||
| 5 |
因此tanα=7,tanβ=
| 1 |
| 2 |
所以tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
7+
| ||
1-7×
|
(2)tan(α+2β)=tan[(α+β)+β]=
-3+
| ||
1-(-3)×
|
又0<α<
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
所以由tan(α+2β)=-1得α+2β=
| 3π |
| 4 |
点评:本题主要考查正切的和角公式与转化思想.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
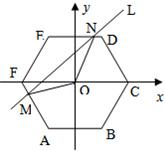 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
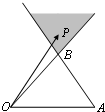 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是