摘要: 已知椭圆的左.右焦点分别为F1.F2.短轴端点分别为A.B.且四边形F1AF2B是边长为2的正方形 (I)求椭圆的方程, (II)若C.D分别是椭圆长轴的左.右端点.动点M满足.连结CM交椭圆于P.证明为定值,K^S*5U.C#O% 的条件下.试问在x轴上是否存在异于点C的定点Q.使以线段MP为直径的圆恒过直线DP.MQ的交点.若存在.求出Q的坐标.若不存在.说明理由
网址:http://m.1010jiajiao.com/timu_id_3949460[举报]
(本题满分13分)
已知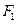 、
、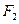 分别是椭圆
分别是椭圆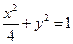 的左、右焦点。
的左、右焦点。
(I)若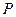 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,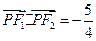 ,求点P的坐标;
,求点P的坐标;
(II)设过定点M(0,2)的直线 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且 为锐角(其中
为锐角(其中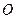 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率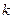 的取值范围。
的取值范围。
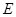 :
: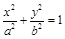 (
(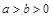 )过点
)过点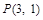 ,其左、右焦点分别为
,其左、右焦点分别为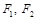 ,且
,且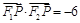 .
. 的方程;
的方程; 是直线
是直线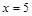 上的两个动点,且
上的两个动点,且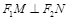 ,则以
,则以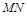 为直径的圆
为直径的圆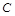 是否过定点?请说明理由.
是否过定点?请说明理由. :
: 左右焦点
左右焦点 、
、 的动直线
的动直线 相交于
相交于 点,与椭圆
点,与椭圆 分别交于
分别交于 不同四点,直线
不同四点,直线 的斜率
的斜率 、
、 、
、 、
、 满足
满足 .已知当
.已知当 轴重合时,
轴重合时, ,
, .
. 的方程;
的方程; ,使得
,使得 为定值.若存在,求出
为定值.若存在,求出 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
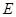 :
: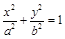 (
(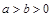 )过点
)过点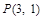 ,其左、右焦点分别为
,其左、右焦点分别为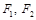 ,且
,且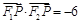 .
.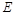 的方程;
的方程;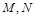 是直线
是直线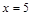 上的两个动点,且
上的两个动点,且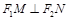 ,则以
,则以 为直径的圆
为直径的圆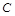 是否过定点?请说明理由.
是否过定点?请说明理由.