题目内容
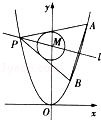
(本题满分13分)如图,分别过椭圆 :
: 左右焦点
左右焦点 、
、 的动直线
的动直线 相交于
相交于 点,与椭圆
点,与椭圆 分别交于
分别交于 不同四点,直线
不同四点,直线 的斜率
的斜率 、
、 、
、 、
、 满足
满足 .已知当
.已知当 轴重合时,
轴重合时, ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)是否存在定点 ,使得
,使得 为定值.若存在,求出
为定值.若存在,求出 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
(1) (2)M、N坐标分别为
(2)M、N坐标分别为 ;
; 为定值
为定值
解析试题分析:(1)由已知条件推导出|AB|=2a=2 ,|CD|=
,|CD|= ,由此能求出椭圆E的方程.
,由此能求出椭圆E的方程.
(2)焦点F1、F2坐标分别为(-1,0),(1,0),当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0),当直线l1,l2斜率存在时,设斜率分别为m1,m2,设A(x1,y1),B(x2,y2),由 ,得(2+3m12)x2+6m12x+3m12?6=0,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|为定值2
,得(2+3m12)x2+6m12x+3m12?6=0,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|为定值2 .
.
(1)当l1与x轴重合时, ,即
,即 , 2分
, 2分
∴l2垂直于x轴,得 ,
, ,(4分)
,(4分)
得 ,
, , ∴椭圆E的方程为
, ∴椭圆E的方程为 . 5分
. 5分
(2)焦点 、
、 坐标分别为(—1,0)、(1,0).
坐标分别为(—1,0)、(1,0).
当直线l1或l2斜率不存在时,P点坐标为(—1,0)或(1,0). 6分
当直线l1、l2斜率存在时,设斜率分别为 ,
, ,设
,设 ,
, ,
,
由 得:
得: ,
,
∴ ,
, .(7分)
.(7分)
 ,
,
同理
 . 9分
. 9分
∵ ,∴
,∴ ,即
,即 .
.
由题意知 , ∴
, ∴ .
.
设 ,则
,则 ,即
,即 , 11分
, 11分
由当直线l1或l2斜率不存在时,P点坐标为(—1,0)或(1,0)也满足此方程,
∴ 点椭圆
点椭圆 上, 12分
上, 12分
∴存在点M、N其坐标分别为 ,使得
,使得 为定值
为定值 . 13分
. 13分
考点:直线与圆锥曲线的综合问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 上的点到点
上的点到点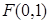 的距离比它到直线
的距离比它到直线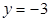 的距离小2.
的距离小2.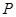 处的切线
处的切线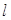 与
与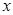 轴交于点
轴交于点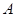 .直线
.直线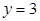 分别与直线
分别与直线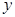 轴交于点
轴交于点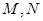 ,以
,以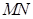 为直径作圆
为直径作圆 ,过点
,过点 ,试探究:当点
,试探究:当点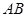 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.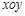 中,已知椭圆的焦点在
中,已知椭圆的焦点在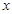 轴上,离心率为
轴上,离心率为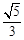 ,且经过点
,且经过点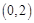 .
.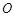 ,设
,设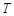 为圆
为圆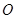 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点,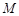 为
为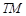 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点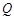 .问:直线
.问:直线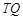 能否与圆
能否与圆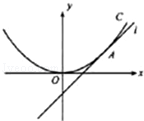
 过点
过点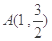 ,两个焦点为
,两个焦点为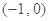 ,
,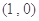 .
.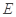 ,
,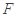 是椭圆
是椭圆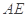 的斜率与
的斜率与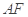 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线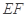 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.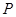 是椭圆
是椭圆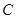 上任一点,点
上任一点,点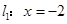 的距离为
的距离为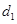 ,到点
,到点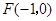 的距离为
的距离为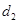 ,且
,且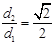 .直线
.直线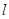 与椭圆
与椭圆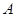 、
、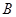 (
(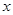 轴上方),且
轴上方),且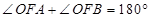 .
.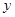 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线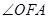 如何变化,直线
如何变化,直线
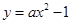 ,直线
,直线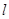 的方程为
的方程为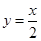 ,点
,点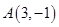 关于直线
关于直线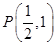 ,点
,点 是抛物线的焦点,
是抛物线的焦点, 是抛物线上的动点,求
是抛物线上的动点,求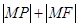 的最小值及此时点
的最小值及此时点 、
、 是抛物线上的动点,点
是抛物线上的动点,点 是抛物线与
是抛物线与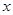 轴正半轴交点,
轴正半轴交点, 是以
是以 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. 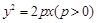 的焦点为
的焦点为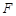 ,点
,点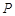 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,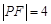 .
.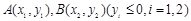 是抛物线上的两点,
是抛物线上的两点,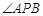 的角平分线与
的角平分线与 轴垂直,求
轴垂直,求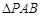 的面积最大时直线
的面积最大时直线 的方程.
的方程.