摘要：是否存在这样的实数a.使函数f(x)＝x2+(3a-2)x+a-1在区间[-1,3]上与x轴恒有一个交点.且只有一个交点.若存在.求出范围.若不存在.说明理 由. 解:若实数a满足条件.则只需f(-1)·f(3)≤0即可. f(-1)·f(3)＝(1-3a+2+a-1)·(9+9a-6+a-1)＝4(1-a)(5a+1)≤0.所以a≤-或a≥1. 检验:(1)当f(-1)＝0时.a＝1.所以f(x)＝x2+x.令f(x)＝0.即x2+x＝0.得x＝0或x＝-1. 方程在[-1,3]上有两根.不合题意.故a≠1. (2)当f(3)＝0时.a＝-.此时f(x)＝x2-x-.令f(x)＝0.即x2-x-＝0.解之得x＝-或x＝3.方程在[-1,3]上有两根.不合题意.故a≠-. 综上所述.a＜-或a＞1.
网址：http://m.1010jiajiao.com/timu_id_3946507[举报]
(本小题满分12分）
已知奇函数，
的图象在x=2处的切线方程为
(I )求
的解析式；
(II)是否存在实数,m,n使得函数
在区间
上的最小值为m，最大值为n.若存在，求出这样一组实数m,n,若不存在，则说明理由.
查看习题详情和答案>>
(本小题满分12分）
已知奇函数，
的图象在x=2处的切线方程为
(I )求
的解析式；
(II)是否存在实数,m,n使得函数
在区间
上的最小值为m，最大值为n.若存在，求出这样一组实数m,n,若不存在，则说明理由.
查看习题详情和答案>>
(本小题满分12分)
已知直线
与双曲线
交于A、B两点，
（1）若以AB线段为直径的圆过坐标原点，求实数a的值。
（2）是否存在这样的实数a，使A、B两点关于直线
对称？说明理由.
查看习题详情和答案>>
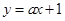与双曲线
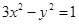交于A、B两点，
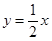对称？说明理由.
，
，如果
,则这样的实数x是否存在？若存在，求出x；若
不存在，说明理由。