摘要：(文)已知曲线C:y＝lnx-4x与直线x＝1交于一点P.那么曲线C在点P处的切线方程是 . 解析:由已知得y′＝-4.所以当x＝1时有y′＝-3.即过点P的切线的斜率k＝-3.又y＝ln1-4＝-4.故切点P.所以点P处的切线方程为y+4＝-3(x-1).即3x+y+1＝0. 答案:3x+y+1＝0 (理)已知函数f(x)＝3x2+2x+1.若∫f(x)dx＝2f(a)成立.则a＝ . 解析:∫(3x2+2x+1)dx＝(x3+x2+x)|＝4. 所以2(3a2+2a+1)＝4.即3a2+2a-1＝0. 解得a＝-1或a＝. 答案:-1或
网址：http://m.1010jiajiao.com/timu_id_3946503[举报]
（理）在直角坐标系xOy中，已知曲线C的参数方程是
（θ是参数），若以坐标原点O为极点，x轴的正半轴为极轴，则曲线C的极坐标方程可写为 ．
（文）若D是由
所确定的区域，则圆x2+y2=4在D内的弧长为 ．
查看习题详情和答案>>
|
（文）若D是由
|
已知曲线C：x2-y|y|=1（|x|≤4）．（1）画出曲线C的图象，
（2）（文）若直线l：y=x+m与曲线C有两个公共点，求m的取值范围；
（理）若直线l：y=kx-1与曲线C有两个公共点，求k的取值范围；
（3）若P（0，p）（p＞0），Q为曲线C上的点，求|PQ|的最小值．
（浙江卷理20文22）已知曲线C是到点P（-
，
）和到直线y=-
距离相等的点的轨迹.L是过点Q（-1，0）的直线，M是C上（不在l上）的动点； A、B在l上，MA
l，MBx轴（如图）.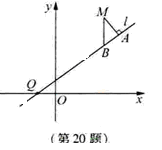 
（Ⅰ）求曲线C的方程；
（Ⅱ）求出直线l的方程，使得
为常数
，
）和到直线y=-
距离相等的点的轨迹.L是过点Q（-1，0）的直线，M是C上（不在l上）的动点； A、B在l上，MA
l，MB
为常数