题目内容
(理)在直角坐标系xOy中,已知曲线C的参数方程是
|
(文)若D是由
|
分析:(理)把曲线C的参数方程化为直角坐标方程,再把直角坐标方程化为极坐标方程.
(文)如图所示,利用两条直线的夹角公式求得∠AOB=
,由弧长公式求得劣弧长AB的值.
(文)如图所示,利用两条直线的夹角公式求得∠AOB=
| π |
| 4 |
解答:解:(理)把曲线C的参数方程是
(θ是参数),化为直角坐标方程可得x2+(y-1)2=1,
即 x2+y2-2y=0,化为极坐标方程为 ρ2-2ρsinθ=0,故答案为:ρ=2sinθ.
(文)如图所示:劣弧长AB即为所求,OA的斜率为
,OB的斜率为-
,
tan∠AOB=|
|=1,∴∠AOB=
,故劣弧长AB为
×r=
×2=
,
故答案为:
.

|
即 x2+y2-2y=0,化为极坐标方程为 ρ2-2ρsinθ=0,故答案为:ρ=2sinθ.
(文)如图所示:劣弧长AB即为所求,OA的斜率为
| 1 |
| 2 |
| 1 |
| 3 |
tan∠AOB=|
| ||||
1+
|
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故答案为:
| π |
| 2 |

点评:本题考查参数方程与普通方程、极坐标方程之间的转化,两直线的夹角公式和弧长公式的应用,求得∠AOB=
,是解题的难点.
| π |
| 4 |

练习册系列答案
相关题目
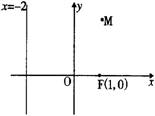
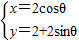 (θ为参数),以原点为极点,以x轴正半轴为极轴建立极坐标系,则圆C的圆心极坐标为 .
(θ为参数),以原点为极点,以x轴正半轴为极轴建立极坐标系,则圆C的圆心极坐标为 .