摘要：某工厂生产某种产品固定成本为2 000万元.并且每生产一单位产品.成本增加10万元.又知总收入K是单位产品数Q的函数.K(Q)＝40Q-Q2.则总利润L(Q)的最大值是 . 解析:总利润L(Q)＝40Q-Q2-10Q-2 000 ＝-(Q-300)2+2 500. 故当Q＝300时.总利润最大值为2 500万元. 答案:2 500万元 题组三 指数函数模型
网址：http://m.1010jiajiao.com/timu_id_3946340[举报]
某工厂生产某种产品，固定成本为20 000元，每生产一件产品成本增加100元，已知总收益R（总收益指工厂出售产品的全部收入，它是成本与总利润的和，单位：元）是年产量（单位：件）的函数.满足关系式：
R=f(Q)=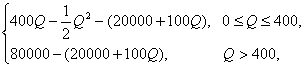
（1）将总利润L（单位：元）表示为Q 的函数;
（2）求每生产多少件产品时、总利润最大？此时总利润是多少？
查看习题详情和答案>>某工厂生产某种产品的固定成本为2 000万元，每生产一单位产品，成本增加10万元，又知总收入k是产品数θ的函数，k(θ)＝40θ－
θ2，则总利润L(θ)的最大值是________．
某工厂生产某种产品x（百台），总成本为G（x）（万元），其中固定成本为2万元，每生产100台增加成本1万元，销售收入R（x）=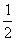
假设该产销平衡，
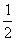假设该产销平衡，（1）要不产生亏损，产量数x应控制在什么范围？
（2）生产多少台时可使利润最大？
（3）求使利润最大时产品的售价.
查看习题详情和答案>>
某工厂生产一种产品的固定成本是20000元，每生产一件产品需要另外投入100元，市场销售部进行调查后得知，市场对这种产品的年需求量为1000件，且销售收入函数