Question

某工厂生产某种产品，固定成本为20 000元，每生产一件产品成本增加100元，已知总收益R（总收益指工厂出售产品的全部收入，它是成本与总利润的和，单位：元）是年产量（单位：件）的函数.满足关系式：

R=f(Q)=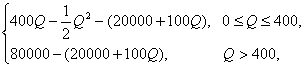

（1）将总利润L（单位：元）表示为Q 的函数;

（2）求每生产多少件产品时、总利润最大？此时总利润是多少？

Answer 1

解析：（1）根据题意，总成本应为C=g(Q)=20 000+100Q,

    从而可得总利润函数为L=φ(Q)=

   

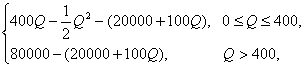
    即L=

    （2）当0≤Q≤400时,

    L=-（Q-300）²-20 000+45 000=-（Q-300）²+25 000.

    此时当Q=300时，L_最大=25 000；

    当Q＞400时，L=60 000-100Q＜60 000-100×400=20 000＜25 000；

    所以，当Q=300时，L_最大=25 000.

    答：每年生产300件产品时，总利润最大，最大利润为25 000元.