摘要:已知数列的前n项和为.对任意n∈N*,都有.且(k∈N*).则的值为 .k的值为 . 答案:-1 14 解析:当n=1时..可知(a1=-l.当n ≥ 2时. .可知.即{an}是等比数列.得 an=-1(-2)n-1.得a1=-1.a2=2.a3=-4.a4=8.a5=-16.因为S3<0.S4=5.S5=-8.S6=20.所以当k=4时符合题意.本题主要考查数列的通项公式的求解问题.知道an与Sn的关系式求数列的通项公式问题是一类热点问题.经常考查.在复习时要加强这类题的学习与总结. 答案:D.
网址:http://m.1010jiajiao.com/timu_id_3942857[举报]
 的前n项和为
的前n项和为 ,对任意
,对任意 ,点
,点 都在函数
都在函数 的图像上。
的图像上。 的通项公式;
的通项公式; ,且数列
,且数列 是等差数列,求非零常数p的值;
是等差数列,求非零常数p的值; ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所
对所 有都成立的最小正整数m。
有都成立的最小正整数m。  的前n项和为
的前n项和为 ,且
,且 .
. ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.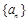 的前n项和为
的前n项和为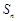 ,
,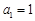 ,且
,且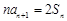 ,数列
,数列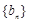 满足
满足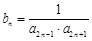 ,数列
,数列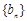 的前n项和为
的前n项和为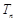 (其中
(其中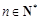 ).
).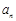 和
和 ,不等式
,不等式 恒成立,求实数
恒成立,求实数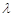 的取值范围
的取值范围