摘要:10.求下列函数的定义域.值域及单调性. (1)y=6+x-2x2, (2)y=-|x|. [解析] (1)函数的定义域为R. 令u=6+x-2x2.则y=u. ∵二次函数u=6+x-2x2=-22+. ∴函数的值域为. 又∵二次函数u=6+x-2x2的对称轴为x=. 在上u=6+x-2x2是减函数. 在上是增函数.又函数y=u是减函数. ∴y=6+x-2x2在上是增函数. 在上是减函数. (2)定义域为x∈R. ∵|x|≥0.∴y=-|x|=|x|≥0=1. 故y=-|x|的值域为{y|y≥1}. 又∵y=-|x|是偶函数. 且y=-|x|= 所以函数y=-|x|在(-∞.0]上是减函数.在[0.+∞)上是增函数.
网址:http://m.1010jiajiao.com/timu_id_3941556[举报]
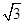 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点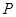 ,作扇形的内接矩形
,作扇形的内接矩形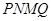 ,使点
,使点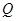 在
在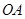 上,点
上,点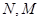 在
在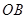 上,设矩形
上,设矩形 ,
,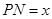 ,将
,将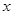 的函数关系式;
的函数关系式;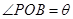 ,将
,将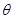 的函数关系式;
的函数关系式;

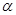 的函数关系式:
的函数关系式: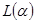 ;
;