摘要:将圆O: 上各点的纵坐标变为原来的一半 , 得到曲线C. (1) 求C的方程; (2) 设O为坐标原点, 过点的直线l与C交于A.B两点, N为线段AB的中点, 延长线段ON交C于点E. 求证: 的充要条件是. 解: (1)设点, 点M的坐标为,由题意可知------ 又∴. 所以, 点M的轨迹C的方程为.------ (2)设点, , 点N的坐标为, ㈠当直线l与x轴重合时, 线段AB的中点N就是原点O, 不合题意,舍去; ------ ㈡设直线l: 由消去x, 得------① ∴------ ∴, ∴点N的坐标为.------ ①若, 坐标为, 则点E的为, 由点E在曲线C上, 得, 即 ∴舍去). 由方程①得 又 ∴.------ ②若, 由①得∴ ∴点N的坐标为, 射线ON方程为: , 由 解得 ∴点E的坐标为 ∴. 综上, 的充要条件是.
网址:http://m.1010jiajiao.com/timu_id_3938372[举报]
(本小题12分) 将圆O:  上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线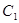 、抛物线
、抛物线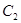 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.
(1)求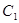 ,
,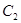 的标准方程;
的标准方程;
(2)请问是否存在直线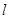 满足条件:①
过
满足条件:①
过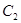 的焦点
的焦点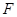 ;②与
;②与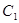 交于不同两
交于不同两
点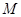 ,
,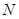 ,且满足
,且满足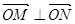 ?若存在,求出直线
?若存在,求出直线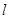 的方程; 若不存在,说明
的方程; 若不存在,说明
理由.
查看习题详情和答案>>
(本小题12分) 将圆O: 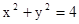 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线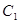 、抛物线
、抛物线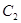 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.
(1)求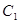 ,
,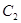 的标准方程;
的标准方程;
(2)请问是否存在直线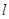 满足条件:① 过
满足条件:① 过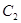 的焦点
的焦点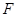 ;②与
;②与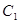 交于不同两
交于不同两
点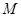 ,
,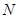 ,且满足
,且满足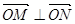 ?若存在,求出直线
?若存在,求出直线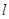 的方程; 若不存在,说明
的方程; 若不存在,说明
理由.
(本小题12分) 将圆O: 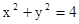 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线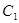 、抛物线
、抛物线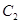 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.
(1)求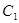 ,
,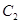 的标准方程;
的标准方程;
(2)请问是否存在直线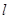 满足条件:① 过
满足条件:① 过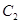 的焦点
的焦点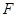 ;②与
;②与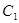 交于不同两
交于不同两
点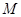 ,
,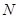 ,且满足
,且满足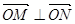 ?若存在,求出直线
?若存在,求出直线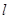 的方程; 若不存在,说明
的方程; 若不存在,说明
理由.
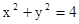 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线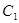 、抛物线
、抛物线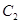 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.(1)求
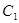 ,
,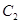 的标准方程;
的标准方程;(2)请问是否存在直线
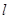 满足条件:① 过
满足条件:① 过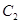 的焦点
的焦点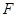 ;②与
;②与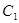 交于不同两
交于不同两点
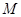 ,
,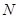 ,且满足
,且满足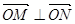 ?若存在,求出直线
?若存在,求出直线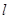 的方程; 若不存在,说明
的方程; 若不存在,说明理由.