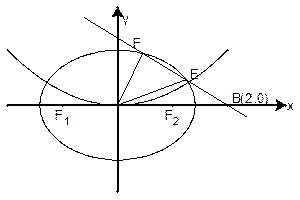摘要:4.中心在原点.焦点在轴上的椭圆.离心率.此椭圆与直线 交于.两点.且(其中为坐标原点).求椭圆的方程. 解:设椭圆方程为. 因为.所以.即. 所以椭圆方程化简为.即为. 由消去得. 设..则.. 又因为.所以.即. 所以.整理得 . 所以.化简得. 故所求椭圆方程为.
网址:http://m.1010jiajiao.com/timu_id_3938371[举报]
如图中心在原点,焦点在![]() 轴上的椭圆,离心率
轴上的椭圆,离心率![]() ,且经过抛物线
,且经过抛物线![]() 的焦点.
的焦点.
(I)求椭圆的标准方程;
(II)若过点B(2,0)的直线L(斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求![]() OBE与
OBE与![]() OBF面积1:2,求直线L的方程。
OBF面积1:2,求直线L的方程。
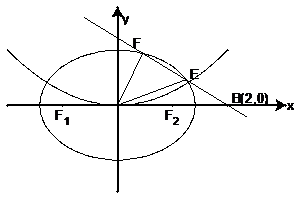 |
查看习题详情和答案>>
已知中心在原点,焦点在 轴上的椭圆,离心率
轴上的椭圆,离心率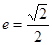 ,且经过抛物线
,且经过抛物线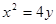 的焦点.
的焦点.
(1)求椭圆的标准方程;
(2)若过点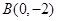 的直线
的直线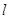 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点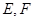 (
(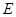 在
在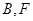
之间),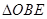 与
与 面积之比为
面积之比为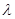 ,求
,求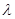 的取值范围.
的取值范围.
查看习题详情和答案>>
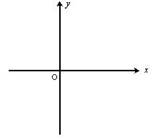 如图中心在原点,焦点在
如图中心在原点,焦点在![]() 轴上的椭圆,离心率
轴上的椭圆,离心率![]() ,且经过抛物线
,且经过抛物线![]() 的焦点.
的焦点.
(I)求椭圆的标准方程;
(II)若过点B的直线![]() (斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求
(斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求![]() OBE与
OBE与![]() OBF面积之比的取值范围.
OBF面积之比的取值范围.
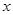 轴上的椭圆,离心率
轴上的椭圆,离心率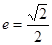 ,且经过抛物线
,且经过抛物线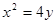 的焦点.
的焦点.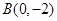 的直线
的直线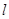 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点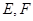 (
(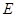 在
在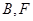
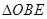 与
与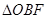 面积之比为
面积之比为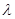 ,求
,求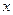 轴上的椭圆,离心率
轴上的椭圆,离心率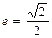 ,且经过抛物线
,且经过抛物线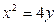 的焦点.
的焦点. 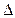 OBE与
OBE与