题目内容
已知函数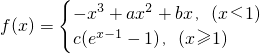 在
在 处取到极值
处取到极值
(Ⅰ)当c=e时,方程 恰有三个实根,求实数k的取值范围;
恰有三个实根,求实数k的取值范围;
(Ⅱ)若函数y=f(x)的图象上存在两点A,B使得 (O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围.
(O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围.
 解:(I)当x<1时,f′(x)=-3x2+2ax+b.
解:(I)当x<1时,f′(x)=-3x2+2ax+b.由极值点的必要条件可知
 是方程f′(x)=0的两根,
是方程f′(x)=0的两根,则0+
 =
= ,0×
,0× =-
=- ,解得a=1,b=0.
,解得a=1,b=0.∴当c=e时,
 …4分.
…4分.当x≥1时,f′(x)=
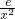 >0,此时函数在[1,+∞)上是增函数,如图,又当x=
>0,此时函数在[1,+∞)上是增函数,如图,又当x= 时,f(x)取得极大值
时,f(x)取得极大值 ,
,由图象知当k∈(0,
 )时,函数y=k与y=f(x)有3个不同的交点,
)时,函数y=k与y=f(x)有3个不同的交点,即方程有3个实根.
故实数k的取值范围为(0,
 )…8分.
)…8分.(II)由(I)知,f(x)=
 ,
,根据条件得A,B的横坐标互为相反数,不妨设A(-t,-t3+t2),B(t,f(t)),(t>0).
若t<1,则f(t)=-t3+t2,
由
 ,即-t2+(-t3+t2)(-t3+t2)=0,
,即-t2+(-t3+t2)(-t3+t2)=0,即-1+(-t+1)2=0.此时t=0或2,不合,舍去;
若t≥1,则f(t)=c(et-1-1).
由于AB的中点在y轴上,且∠AOB是直角,所以B点不可能在x轴上,即t≠1.
同理由
 ,即-t2+(-t3+t2)•c(et-1-1)=0,
,即-t2+(-t3+t2)•c(et-1-1)=0,∴c=
 …12分.
…12分.由于函数g(t)=
 (t>1)的值域是(-∞,0),
(t>1)的值域是(-∞,0),∴实数c的取值范围是(-∞,0)…14分.
分析:(I)当x<1时,先对函数f(x)进行求导,由题意知
 是方程f'(x)=0的两实根,由韦达定理可求出a,b的值.将方程转化为函数y=k与y=f(x),将方程根的问题转化为函数图象交点问题解决.
是方程f'(x)=0的两实根,由韦达定理可求出a,b的值.将方程转化为函数y=k与y=f(x),将方程根的问题转化为函数图象交点问题解决.(II)根据分段函数,分类讨论,利用
 ,结合函数思想即可求实数c的取值范围.
,结合函数思想即可求实数c的取值范围.点评:本题主要考查函数的单调性、极值点与其导函数之间的关系,以及研究方程根的个数问题,此类问题首选的方法是图象法即构造函数利用函数图象解题,其次是直接求出所有的根.

练习册系列答案
相关题目
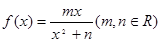 在
在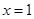 处取到极值
处取到极值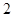
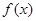 的解析式;
的解析式;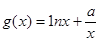 ,若对任意的
,若对任意的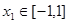 ,总存在
,总存在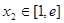 ,使得
,使得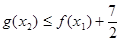 ,求实数
,求实数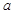 的取值范围.
的取值范围.
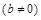 在
在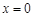 处取到极值2.
处取到极值2.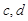 的值;
的值;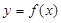 的所有切线与直线
的所有切线与直线 垂直的条数;
垂直的条数;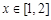 ,均存在
,均存在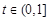 ,使得
,使得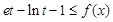 ,试求
,试求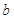 的取值范围.
的取值范围. 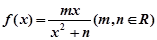 在
在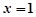 处取到极值2
处取到极值2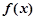 的解析式;
的解析式;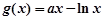 .若对任意的
.若对任意的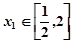 ,总存在唯一的
,总存在唯一的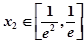 ,使得
,使得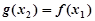 ,求实数
,求实数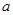 的取值范围.
的取值范围.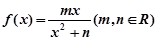 在
在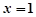 处取到极值2
处取到极值2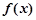 的解析式;
的解析式;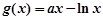 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的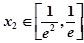 ,使得
,使得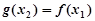 ,求实数
,求实数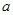 的取值范围.
的取值范围.