题目内容
已知函数![]() 在
在![]() 处有极值.
处有极值.
(Ⅰ)求实数![]() 值;
值;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)令![]() ,若曲线
,若曲线![]() 在
在![]() 处的切线与两坐标轴分别交于
处的切线与两坐标轴分别交于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),求
为坐标原点),求![]() 的面积.
的面积.
(1)![]() (2)
(2)![]() 的单调减区间为
的单调减区间为![]() ,
,![]() 的单调增区间为
的单调增区间为![]()
(3)2
解析:
(Ⅰ)因为![]() ,
,![]()
所以![]() .………………………………………………2分
.………………………………………………2分
由![]() ,可得
,可得 ![]() ,
,![]() .
.
经检验![]() 时,函数
时,函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() .………………………………………………………………5分
.………………………………………………………………5分
(Ⅱ)![]() ,
,
![]()
![]() .………………………………7分
.………………………………7分
而函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
由表可知,![]() 的单调减区间为
的单调减区间为![]() ,
,![]() 的单调增区间为
的单调增区间为![]() .……10分
.……10分
(Ⅲ)由于![]() ,
,
所以![]() ,当
,当![]() 时,
时,![]() ,
,![]() .[来源:Zxxk.Com]
.[来源:Zxxk.Com]
所以切线斜率为![]() ,切点为
,切点为![]() ,
,
所以切线方程为![]() ,即
,即![]() .…………………………………13分
.…………………………………13分
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .
.
所以![]() 的面积
的面积![]() .…………………………………………14分
.…………………………………………14分

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
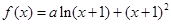 在
在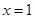 处有极值.
处有极值.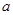 值;
值;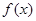 的单调区间;
的单调区间; ,使得不等式
,使得不等式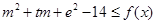 对任意
对任意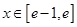 及
及
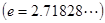
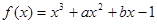 在
在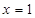 处有极值
处有极值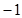 。
。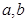 的值;
的值;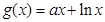 的单调区间。
的单调区间。 在
在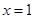 处有极值
处有极值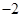 .
.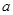 、
、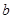 ;
; 与
与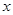 轴所包围的面积。
轴所包围的面积。