摘要: 如图.在四棱锥中.底面是矩形.已知. (Ⅰ)证明平面, (Ⅱ)求异面直线与所成的角的大小, (Ⅲ)求二面角的大小. (Ⅰ)证明:在中.由题设可得 于是.在矩形中..又. 所以平面. (Ⅱ)解:由题设..所以是异面直线与所成的角. 在中.由余弦定理得 由(Ⅰ)知平面.平面. 所以.因而.于是是直角三角形.故. 所以异面直线与所成的角的大小为. (Ⅲ)解:过点P做于H.过点H做于E.连结PE 因为平面.平面.所以.又. 因而平面.故HE为PE再平面ABCD内的射影.由三垂线定理可知. .从而是二面角的平面角. 由题设可得. 于是再中.所以二面角的大小为.
网址:http://m.1010jiajiao.com/timu_id_3933828[举报]
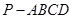 中,底面
中,底面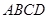 是矩形.已知
是矩形.已知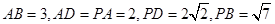 .
.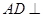 平面
平面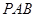 ;
;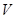 ;
; 的大小为
的大小为 ,求
,求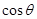 的值.
的值.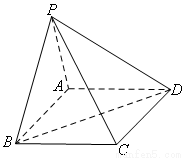
 中,底面
中,底面 是矩形.已知
是矩形.已知 ,
, ,
, ,
,
 平面
平面 ;
; 与
与 所成的角的正切值;
所成的角的正切值; 的正切值.
的正切值.

 如图,在四棱锥
如图,在四棱锥